(图库见这个网页。)
网上有个程序backfract(链接在此Backfract。其作者还发布了一个 围棋程序前端cgoban,百度中搜backfract搜不到,搜cgoban可以搜到),用来显示分形中的曼德勃罗集。这个程序可以自动全屏显示Mandelbrot集的 区域图象,效果不错(我在此显示了一些效果图)。这个程序是运行在_nix/X上的。 网页上介绍其是“随机”选取“有趣的”区域进行显示,但不纯是放大,有时放大,有时接着又缩小。 一些视频网上也有称放大10的“N”次方倍的分形视频,视频放一会就没了。我想能否自己无穷放大,至少尽量放大。
数学上,Mandelbrot集有两种定义。 在《混沌分形及其应用》、《分形的计算机图象及其应用》中大致是这样说的: Mandelbrot集与另一种集合Julia集有联系。记以点c为参数的二次映射$ f_{c} = z^2 + c $ , 复平面任意一点c都各有相应的Julia集, 有的点c相应的Julia集是连通的,有的点c相应的Julia集是不连通的,从这有如下的Mandelbrot集的定义:
Mandelbrot集M是使c的$f_{c}$映射下的Julia集为连通的参数c的集合,即
$$ \begin{aligned} M = \left \{ c \in \mathbb{C} \space \space | \space \space J(f_{c}) \text{为连通的} \right \} \end{aligned} $$ 如果在复平面上把属于连通的Julia集的每个c都标绘出来,则此参数c的集合就是M集的分形图案。这个定义不好用计算机处理,幸好数学上 证明了Mandelbrot集的另一个等价的定义: $$ \begin{aligned} M = \left \{ c \in \mathbb{C} \space \space | \space \space \lim_{n \to \infty} Z_{n} \nrightarrow \infty \right \} \end{aligned} $$ 其中: $$ \begin{aligned} Z_{0} & = 0 \\ Z_{n+1} & = Z_{n}^2 + c \end{aligned} $$ 在这个网页(The Mandelbrot Set)讲了一些实际绘制时的问题处理。(1)判断无穷 数学上可以证明Mandelbrot集完全被包含在以原点为中心,半径为2的闭圆盘内,即: $$ \begin{aligned} M \subset \left \{ c \in \mathbb{C} \space \space | \space \space \left| c \right| \leqslant 2 \right \} \end{aligned} $$ 所以如果迭代中间结果模大于2了,则继续迭代肯定趋于无穷了。因此用模2作一个阈值。
(2)迭代次数 上述网页的作者用了个50次的例子。但我遇到过迭代50次与迭代200或1000次结果不同的情形。所以这个问题的数学根据我还不太清楚。
(3)着色 实际上Mandelbrot集只是中间那个(黑色)形状的部分。其外的点都不属于Mandelbrot集。简单地绘制一个属于或不属于的黑白图象 没太多好看。我们通常看到的的颜色丰富的各种细节有赖于着色。常见用“逃逸”的点的迭代次数取模来选取颜色。(另有的类似等高线绘制,这里不用。) 但简单的着色比不了象backfract这样的程序的效果。
(计算绘图窗口坐标$(i,j)$的点是否属于M集并着色的伪码):
$x_{0} = $ left_coord + delta* $i$;
$y_{0} = $ above_coord - delta* $j$;
$ x = x_{0}$ ; // or $ x = 0 $
$ y = y_{0}$ ; // or $ y = 0 $
int $ k = 0 $ ;
while( $ k \lt $ MAX_ITERATION )
{
real = $ x^2 - y^2 + x_{0} $;
imag = $ 2xy + y_{0} $ ;
$ {|z|}^2 = $ real*real + imag*imag ;
if( $ {|z|}^2 \gt 4 $ )
break;
else{ $ x = $ real; $ y = $ imag; }
$k$ ++;
}
if( $ k \lt $ MAX_ITERATION )
SetPixel(hdc, $i$, $j$ , colors[ $k$ %50]) ;
else
SetPixel(hdc, $i$, $j$ , RGB(0, 0, 0)) ;
$x_{0} = $ left_coord + delta* $i$;
$y_{0} = $ above_coord - delta* $j$;
$ x = x_{0}$ ; // or $ x = 0 $
$ y = y_{0}$ ; // or $ y = 0 $
int $ k = 0 $ ;
while( $ k \lt $ MAX_ITERATION )
{
real = $ x^2 - y^2 + x_{0} $;
imag = $ 2xy + y_{0} $ ;
$ {|z|}^2 = $ real*real + imag*imag ;
if( $ {|z|}^2 \gt 4 $ )
break;
else{ $ x = $ real; $ y = $ imag; }
$k$ ++;
}
if( $ k \lt $ MAX_ITERATION )
SetPixel(hdc, $i$, $j$ , colors[ $k$ %50]) ;
else
SetPixel(hdc, $i$, $j$ , RGB(0, 0, 0)) ;
一般的浮点运算有IEEE 754描述,计算机体系结构的书会涉及。还有书如《浮点计算编程原理、实现与应用》(刘纯根著)进行论述。网上有篇 著名的文章:What Every Computer Scientist Should Know About Floating-Point Arithmetic.
本文前后涉及3个程序:
第一个是用机器浮点double类型、VC++绘制Mandelbrot集;另可用“橡皮筋”选取区域放大各局部;
第二个在以上代码中加入作者float算法实现,比较上述机器浮点运算结果;但尚未修改完成“橡皮筋”选取放大功能;
第三个是未用图形界面,纯比较笔者float算法实现的计算结果和GMP分数运算结果的一致性的程序。
最初3个程序是在(虚拟机)Win XP + VC++6环境下开发的,后来升级到(虚拟机)Win7 + vs2015环境,有略微的修改。 这里两个版本都提供:
VC++6版本 vs2015版本
(代码未加整理,:-()
第1个程序
(1)double实现这个运算部分代码和伪码差不多了:
my_mandel_test_3(machine_float)\my_mandel_testView.cpp:
for(i = 0; i < w; i++)
{
for(j = 0; j < h; j++)
{
BOOL b_is_boundary = FALSE;
if(delta_w > delta_h)
{
if( j == (int)( (h*delta - (old_above_coordinate- \
old_below_coordinate))/(2*delta) )
|| j == ( h-(int)( (h*delta - (old_above_coordinate- \
old_below_coordinate))/(2*delta) ) )
)
b_is_boundary = TRUE;
}
else
{
if( i == (int)( (w*delta - (old_right_coordinate- \
old_left_coordinate))/(2*delta) )
|| i == ( w-(int)( (w*delta - (old_right_coordinate- \
old_left_coordinate))/(2*delta) ) )
)
b_is_boundary = TRUE;
}
double x0 = left_coordinate + delta * (double)i;
double y0 = above_coordinate - delta * (double)j;
double x = x0;
double y = y0;
int k = 0;
#define MAX_ITERATION 1000
while(k < MAX_ITERATION)
{
double real_part = x*x-y*y+x0;
double imaginary_part = 2*x*y+y0;
double z_abs_square = real_part*real_part + imaginary_part*imaginary_part;
if(z_abs_square > 4.0)
{
break;
}
else
{
x = real_part;
y = imaginary_part;
}
k++;
}
if(k < MAX_ITERATION)
{
//unsigned long colors[16] =
unsigned long colors[50] =
{
RGB(0xDE , 0xB8 , 0x87),
...
RGB(0x19 , 0x19 , 0x70 )
};
//SetPixel(hdc, i, j , colors[k%16]);
SetPixel(hdc, i, j , colors[k%50]);
if(b_is_boundary)
SetPixel(hdc, i, j , RGB(255, 255, 255));
}
else
{
SetPixel(hdc, i, j , RGB(0, 0, 0));
if(b_is_boundary)
SetPixel(hdc, i, j , RGB(255, 255, 255));
}
}
}
运行图如:(为避免太占版面,下面是网页显示比例缩小了的;原比例的在此。 也可右键下载图片到本地看。)
选取的放大区域与绘图窗口比例可能不一致,所以将其作一定的延展来适应绘图窗口,让整个绘图窗口的像素点都有图象。上面图象 中的两道白线内部即为用户选取的区域(小图可能有些显示不清,可看原图),相对绘图窗口可能过于扁平或过于瘦高。上面代码中 b_is_boundary的判断处理即是为此。
(程序运行后产生两个中间文本文件draw_coordinates.txt和arguments.txt,下次运行前要把它们删去。)
机器浮点,二进制精度53位,相当于(十进制)小数点后约16位。起始坐标上下、左右均为约(-2,2)量级,若每次选取放大的 区域线度约为原图象的十分之一,那么可以发现大约16次后图象基本上就“马赛克”了。仅仅放大16次,离无穷放大太远了。 而且,后面还将看到机器浮点运算的误差累积在约40次迭代后就已出现明显差误的log记录。
第2个程序
(2) my floats实现由于计算中仅用了乘法和加法,对有限位小数应该可以作完全精确的计算。按照小学运算的方法即可。为了只需计算有限位的小数, 只使用有限位的起始坐标和有限位的步进值,后者通过规定图象宽度高度为特定值,如500、512、800、1000、1024,从而像素代表的点 之间间距也由简单的有限位小数来表示。
所以我在View.cpp中修改了代码,只支持这些特定值。
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.cpp:
if (!(w == 200 || w == 250 || w == 400 || w == 500
|| w == 800 || w == 1000 /*|| w == 1024*/)
|| !(h == 200 || h == 250 || h == 400 || h == 500
|| h == 800 || h == 1000 /*|| h == 1024*/)
)
{
AfxMessageBox(L"width and height not supported");
return;
}
char* one_w_strI = (w == 200) ? "0.005" : (
w == 250 ? "0.004" : (
w == 400 ? "0.0025" : (
w == 500 ? "0.002" : (
w == 800 ? "0.00125" : (
w == 1000 ? "0.001" : ("error characters")
)
)
)
)
);
char* one_h_strI = (h == 200) ? "0.005" : (
...
读者可能还需在View.h中改代码,设置符合上述规定的合适你显示区域的程序窗口宽高:
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.h:
#define DEFAULT_CLIENT_AREA_WIDTH 500//1000 #define DEFAULT_CLIENT_AREA_HEIGHT 250// 800
起始坐标则是x:-2.5到2.5,y:-2.0到2.0:
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.h:
fI fI_left_coord("-2.25");
fI fI_right_coord("2.25");
fI fI_above_coord("2.0");
fI fI_below_coord("-2.0");
加入了实现my floats的三个新文件my_floats.h、my_floatI.cpp、my_floatII.cpp和几个辅助函数。(我在VC6编译项目时有时会报不通过, 把文件重新加入工程一次后又通过了,在vs2015上则完全通不过,报nafxcwd.lib/uafxcwd.lib与libcmtd.lib中有重复定义。遇到这种情况 可能得调整一下工程,在项目的link选项的input栏中先忽略这两个库,然后在其他依赖库中按如上先后顺序加入这两个库。) 我先后用了 两种数据结构来实现float数类,由于实现了前一种后想到后一种可能更好,所以先后完成了两种实现。
实现一:
my_floats.h:
class float_number{
public:
bool minus;
char* number; //in absolute value form
int point_pos;
...
};
实现二:
my_floats.h:
class floatII{
public:
bool minus; //with '-' sign?
char* digits; //no '.' inside
int point_pos_r; //counting from the right side
...
};
有时简记为:
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.cpp:
两者都用单独的成员minus表示正负,所以数字字符串(number或digits)中都不再带符号。区别一是实现前一种时数字字符串中还保留着小数点,
这在后者中去掉了;区别二是小数点的位置,前者是从左到右数的(point_pos),后者则改为从右往左数了(point_pos_r)。由此代码实现起来
后一种简洁一点。这两种实现可以互相比较结果,进行验证。这是验证的方法之二。不过这两者的算法核心是一样的代码,所以可能验证的功能因此有限。
完全的验证还有赖于下面第3个实现了与GMP计算结果对照的程序,作为验证的方法之三,也可以说是真正的验证。(验证方法一是一种局部的验证,
只验证加法,即在作加法后作逆运算回去,看结果是否正确还原。这个没怎么用。)
typedef float_number fI; typedef floatII fII;
实现了float类,以fI实现为例,运算代码变成了大致这样子:(实际的代码由于要相互比较,代码间会互相穿插。这里以早期代码版本为例。)
my_mandel_test_my_floats_0\my_mandel_testView.cpp:
fI fI_left_coord ("-2.25");
fI fI_right_coord( "2.25");
fI fI_above_coord( "2.0" );
fI fI_below_coord("-2.0" );
fI delta_wI, delta_hI, deltaI;
#if 1
fI w_factorI(one_w_strI);
fI h_factorI(one_h_strI);
delta_wI = (fI_right_coord - fI_left_coord ) * w_factorI;
delta_hI = (fI_above_coord - fI_below_coord) * h_factorI;
if(delta_wI > delta_hI)
deltaI = delta_wI;
else
deltaI = delta_hI;
#endif
#if 1
fI x0I(fI_left_coord );
fI y0I(fI_above_coord);
fI aI("2");
fI threshold("4.0");
#endif
#if 1
for(i = 0; i < w; i++)
{
y0I = fI_above_coord;
for(j = 0; j < h; j++)
{
fI xI("0");
fI yI("0");
int k = 0;
#define MAX_ITERATION 10//20//100
while(k < MAX_ITERATION)
{
fI real_part = xI*xI-yI*yI+x0I;
fI imaginary_part = aI*xI*yI +y0I;
fI z_abs_square = real_part*real_part + imaginary_part*imaginary_part;
if(z_abs_square > threshold)
{
break;
}
else
{
xI = real_part;
yI = imaginary_part;
}
k++;
}
if(k < MAX_ITERATION)
{
SetPixel(hdc, i, j , colors[k%50]);
}
else
{
SetPixel(hdc, i, j , RGB(0, 0, 0));
}
y0I = y0I - deltaI;
}
x0I = x0I + deltaI;
}
#endif
fII代码与此类似,基本上只是把I换成II或者加个II后缀罢了。
运行效果图:(现在是可以看到程序在一个一个像素写屏。下面是前后两幅图象。)
下面对log文件内容图示说明:
(蓝色线框依次标记出窗口坐标,复平面上坐标(字串有fI和fII两种形式),迭代序数,退出计算循环时总迭代次数)
(红色线框依次标记出机器浮点算出的实部、虚部、z的模方)
(绿色线框依次标记出我实现的浮点类(fI和fII,结果相等)作高精度近似计算算出的实部、虚部、z的模方的(高精度近似)值)
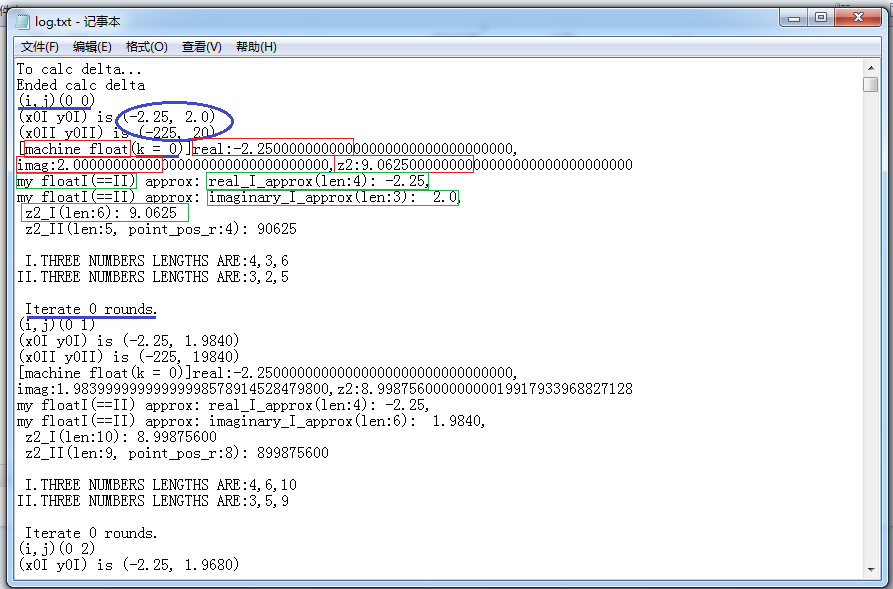
可见位于(0 0)这个点第1次迭代即退出了循环,在M集的外边。然后计算下一个点(0 1)。
下面再举位于(16 125)这个点为例:
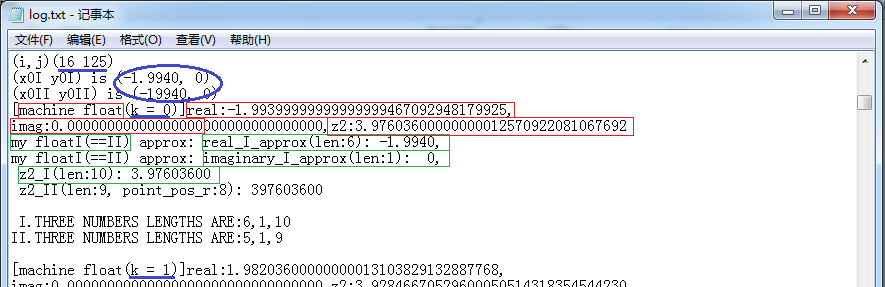
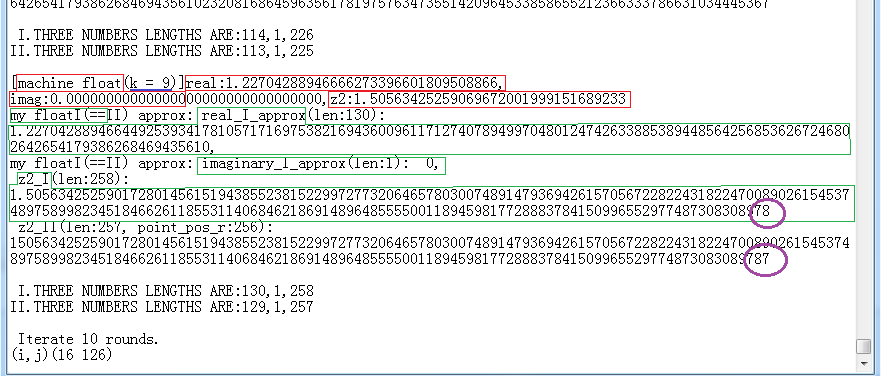
(数字末尾紫色线框标记出的内容不一样,不是计算结果不等,是结果字串长200多位,我这里最大只打印到200位。fI表示比fII表示多了一个 小数点'.'字符,所以少打印一位。)
可见位于(16 125)这个点在实轴上,属于M集,所以一直迭代到最大次数(这里是10次)还未超过阈值。不再算了,然后计算下一个点(16 126)。
使用我自己的float类进行精确计算,带来了密集计算。我的代码中运算是直接在OnDraw函数中进行的,这导致程序不响应外部消息。 在Win XP中不响应外部消息也罢,还能看到程序还在一个像素一个像素地写屏;在Win 7中看到程序画了少量像素后就不写屏了,只显示 “程序不响应”。
为了不让密集计算阻塞消息循环(阻塞消息循环,不是阻塞进程;OnDraw函数在主线程中,在其中密集计算会使主线程长久在这个函数中运行, 拖住了(MFC自身实现的)消息循环的进行。),要么另开一个工作线程来进行计算,要么在密集计算中另插入自己的(非阻塞的)消息处理循环。 这里采用了后一种方法。但在关闭窗口时有点问题,进程没有退出,OnDraw还在运行,只好在View中加了OnDestroy函数处理了一下。
有了自己的float类的精确计算,可以发现机器浮点double类型近似计算的误差累积。下面是log例子。 (log文件下载(下面节选部分在log文件最后处))
(由于迭代次数较高,这里my floats用了一定精度的近似值来与机器浮点double的结果作比较,当然,这个精度远远高过double精度。)
这里观察的是坐标(i,j)为(16,125)的点的迭代计算:
k= 0时,结果是一样的;
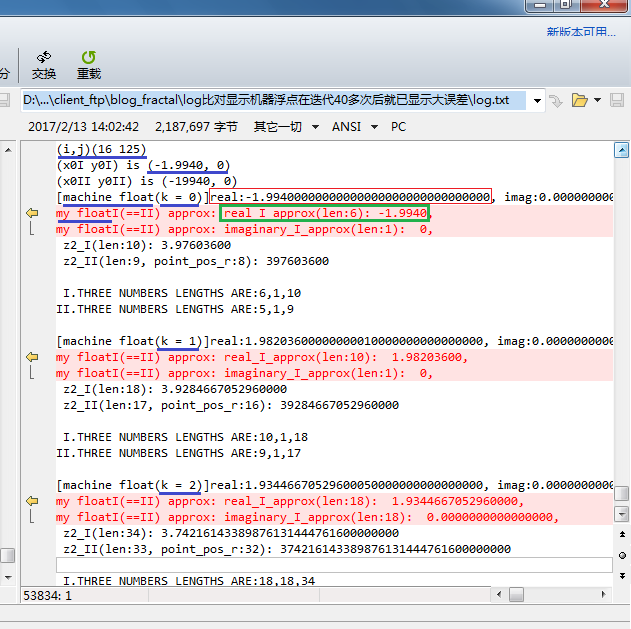
k=40时,差别还不大;
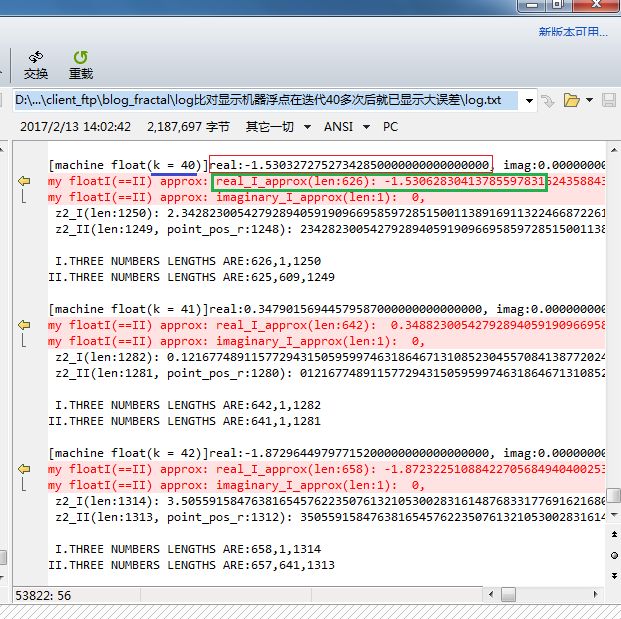
k=47时,小数点后第1位已经有差别了;
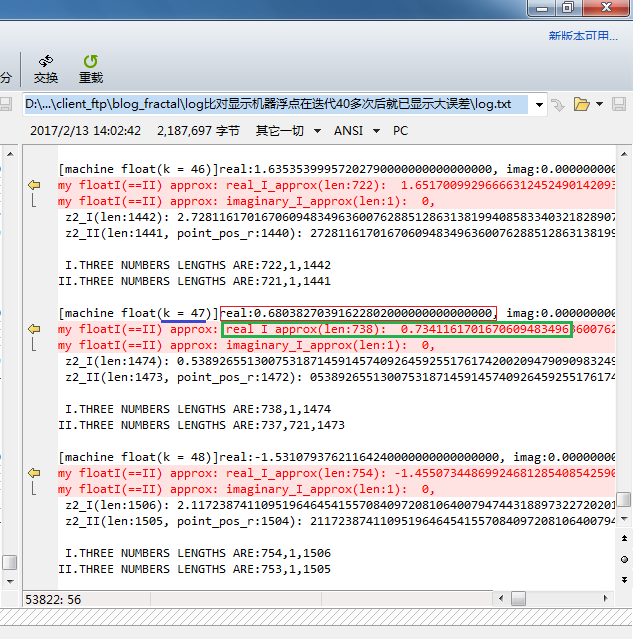
k=52时,已经不能认为两者值接近了;
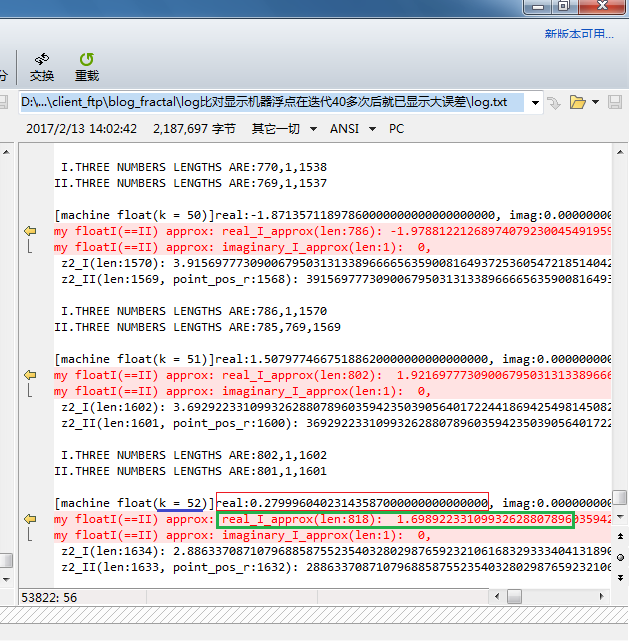
k=53开始,结果正负都不一样了。
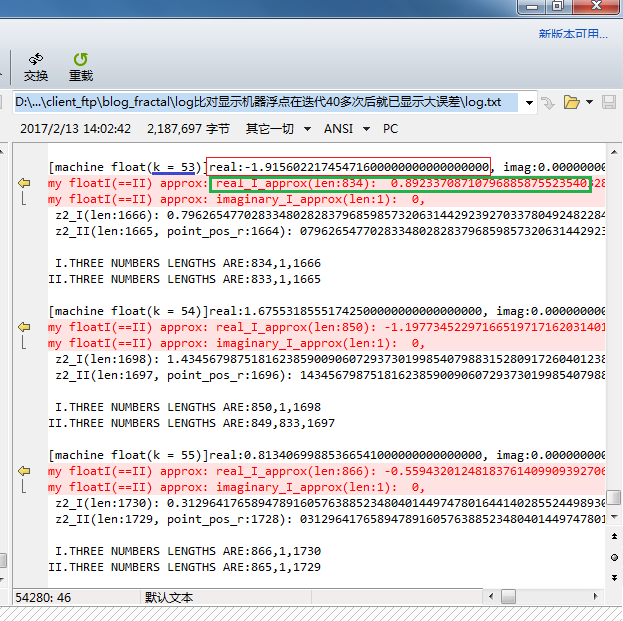
(backfract好象是用long double类型来实现的,但这仍然是太少了。)
区域放大功能这一版本中尚未实现。此外,M集的放大是无穷无尽的,在计算结果得到一定保证之后,我们要考虑究竟怎样放大:手动选取?自动选取? 要怎样呈现M集的图案?
第3个程序
(3) GMP实现GMP是GNU的大数库。我用的GMP库是在虚拟机WinXP上用MinGW编译出来的,然后可以给VC++6下应用程序直接链接使用,再需加一些MinGW中的库 和Windows的库。我在升级/更新程序到虚拟机Win 7+vs2015环境时,这个库仍然可用,仅仅MinGW中的libmsvcrt.a会影响到fprintf函数不能使用, 所以我将vs2015下的代码中的fprintf都改成了fwrite。运行时另外再加上了一些提示需要的VS中VC的库和MS的SDK的库。
GNU的大数库包括GMP、MPFR、MPC库。GMP是大数整数分数库,本来也包含的浮点库功能部分现已可被MPFR代替(GMP手册语);MPFR是大数任意精度 浮点库,基于大数整数库GMP;MPC是大数复数库,基于前两者。(有意思的是构建GCC的话要依赖这些库。)此外,还有一个分支 MPIR从GMP分出来,据说其 着眼于让该大整数库可在Windows下用VS编译,因GMP不行,我这里未用该库。本来我以为要用MPFR库来实现所需功能,所以文件名用了mpfr(mandel_with_mpfr_test), 后来发现只需用GMP库分数部分即可,而且后者以绝对精度进行计算,而不是止于前者的“任意精度”。但文件名没改掉,代码只用了MPFR作了 一处打印日志的功能,其他与MPFR均无关系。
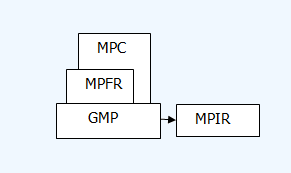
我在WinXP虚拟机上安装了网上下载的MinGW+MSYS离线安装包,按照手册和configure帮助配置、编译了GMP、MPFR(MPFR源码包中有个INSTALL文件讲了 其Windows下三种方式编译:MinGW、Cygwin、vs2015),没有什么太特别的,不过一次只能指定编一个要么静态库要么动态库,我只编译了静态库。 生成的静态库libgmp.a、libmpfr.a可直接给VC++6(及vs2015)使用:
mandel_with_mpfr_test_vs2015\mpfr_inc.h:
其他lib*.a均为编译程序时所需的MinGW中的库。此外运行还需MinGW下的libgcc_s_dw2-1.dll和一些Windows上的dll。
#pragma comment(lib, "libmpfr.a") #pragma comment(lib, "libgmp.a") #pragma comment(lib, "libgcc.a") #pragma comment(lib, "libgcc_s.a") #pragma comment(lib, "libmingwex.a") #pragma comment(lib, "libmsvcrt.a")
GMP是c实现的,有一个C++的包装库可以配置编译,但手册上说了,该c++库一般只能给同一个(c++)编译器的应用程序使用。开发中我发现, 必须用c编译器而非c++编译器处理包含gmp.h的文件,因此mpfr_lib.c必须为.c文件而非.cpp文件。
链接MPFR库有顺序要求,要先libmpfr.a,然后libgmp.a。此外手册上提到VC++使用GMP库在一定情况下必须指示Windows的cl编译器使用/MD选项编译。
(有一个分形的开源项目FractalNow从版本8.0开始加入了使用MPFR计算,该项目基于Qt,我在Ubuntu和WinXp MinGW下编译了该项目。Ubuntu上有 这个项目的包,构建起来相对容易;Windows上其使用的Qt4.8要求MinGW的GCC必须为4.4的,我只好又从网上搜了个GCC4.4的MinGW下载,然后拷贝 以前的MSYS目录使用,此外还下载了一个pthreads-w32的包才完成编译。)
运行图:
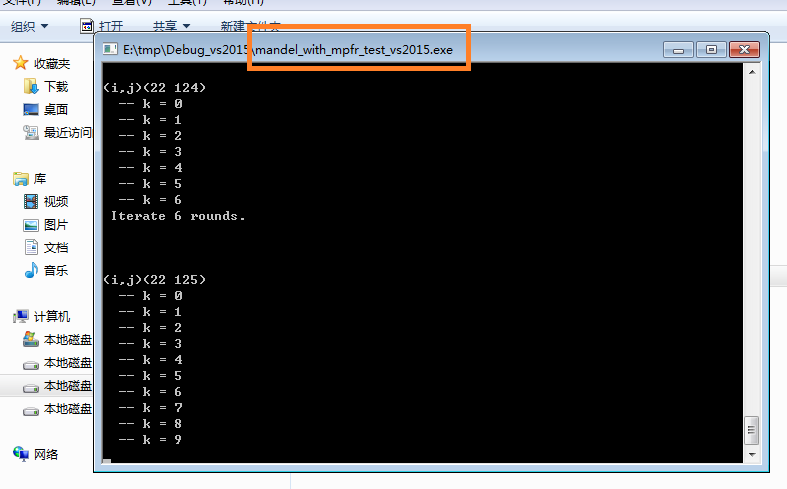
log文件中主要是多了些GMP计算结果和用MPFR打印的内容:
下面这第一张图是坐标(22 0)的点。(如果你不改下载的程序源码,很可能看到的log开头就是这儿,因我调试时是跳过了前面的坐标点,从列22开始的, 代码没整理,没去掉这个。)
蓝、绿、红的线框标识的含义仍同前所述。赭色的是GMP的计算结果用MPFR打印出的小数。多了相应颜色的加粗线框是新增的,打印的是绝对精确值 而非高精度近似值。先后就实部精确值、实部近似值、虚部精确值、虚部近似值、z的模方精确值、z的模方近似值使用GMP对我自己的float实现进行了验证。
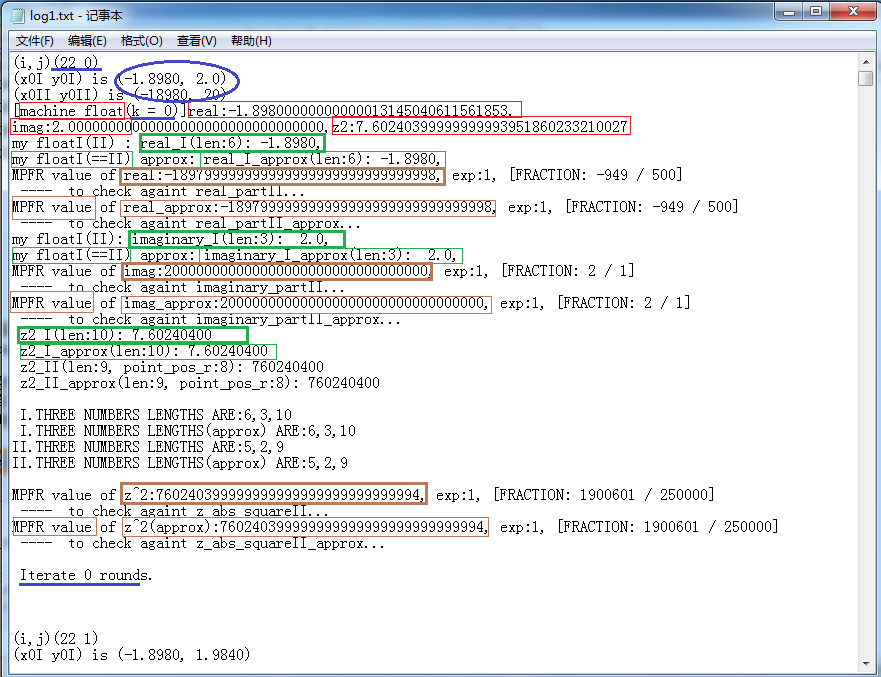
上图循环1次即结束了,log较短。再以坐标(22 125)的点的第k=9次迭代进一步看看,这下log长了,一张图显示不下,而且我这里只好把其中冗长的多行数字
用*行代替。下面第1张完成了实部精确值、近似值的比较:
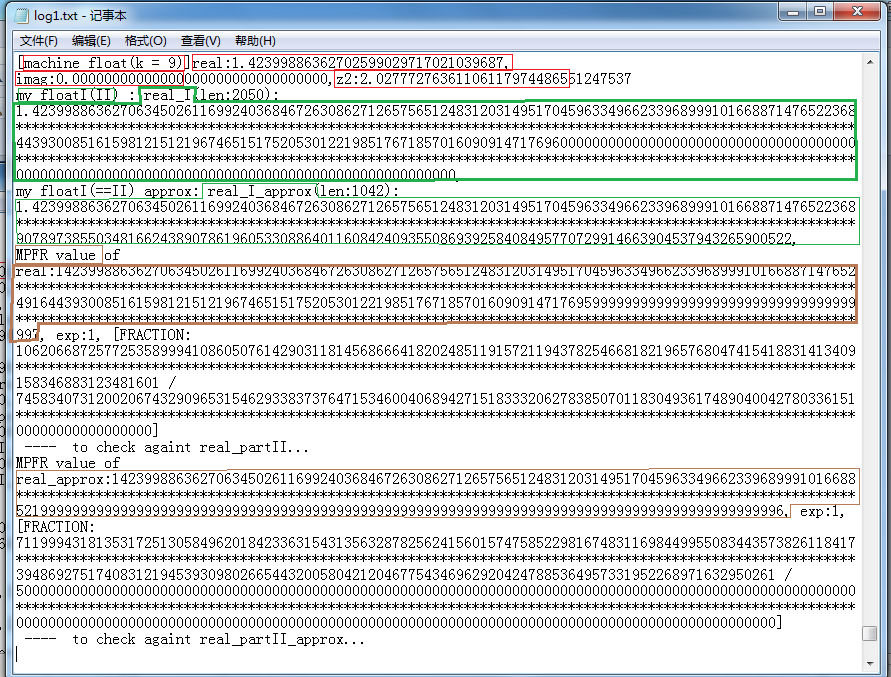
第2张完成了虚部精确值、近似值的比较。因该点在实轴上,虚部为0,所以log很短。
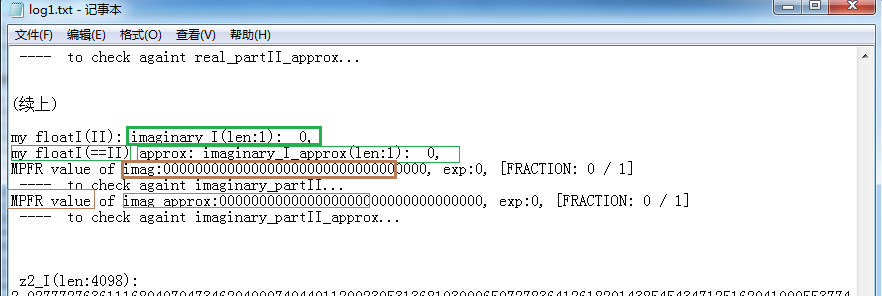
最后第3张中完成了z的模方的精确值、近似值的比较。
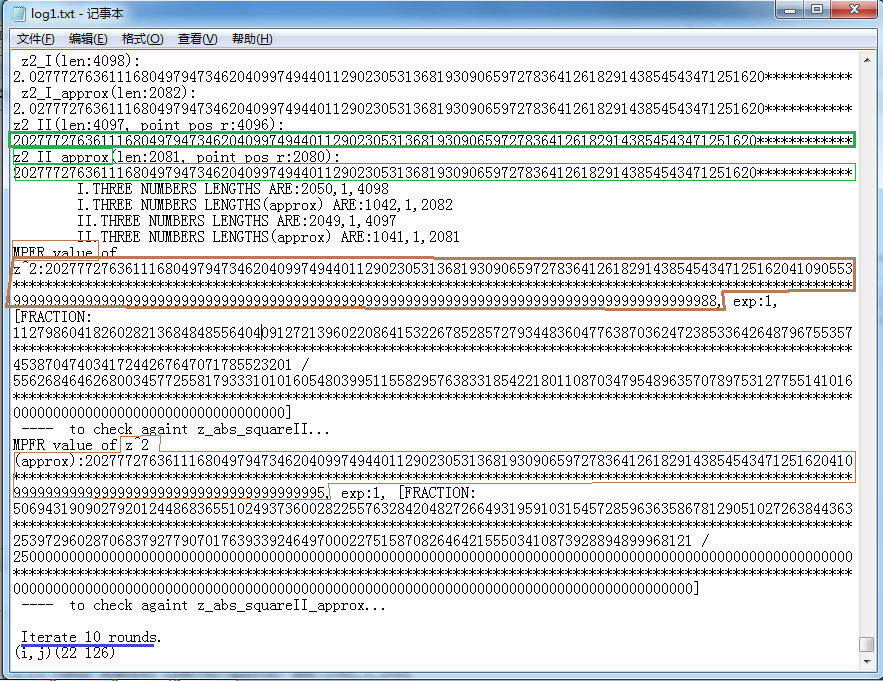
这些图中没标记的“[FRACTION ... / ...]”字样的部分是GMP采用的分数形式表示,即 分子 / 分母,且是不可约的。
这第3个程序没有了图形界面功能,只剩纯粹的计算。代码从View.cpp换到了main.cpp,新增GMP实现的函数均以“GMP_”开头,在mpfr_inc.h和mpfr_lib.c 两个文件中(如上所述,用的mpfr的文件名)。把前面的伪码变成用GMP的代码示意:
(伪码):
x0(left );
y0(above);
a("2");
threshold("4.0");
for(i = 0; i < w; i++)
{
y0 = above;
for(j = 0; j < h; j++)
{
x("0");
y("0");
k = 0;
while(k++ < MAX_ITER)
{
real = x*x-y*y +x0;
imag = a*x*y +y0;
z_square = real*real + imag*imag;
if(z_square > threshold)
break;
else{
x = real;
y = imag;
}
}
y0 = y0 - delta;
}
x0 = x0 + delta;
}
x0(left );
y0(above);
a("2");
threshold("4.0");
for(i = 0; i < w; i++)
{
y0 = above;
for(j = 0; j < h; j++)
{
x("0");
y("0");
k = 0;
while(k++ < MAX_ITER)
{
real = x*x-y*y +x0;
imag = a*x*y +y0;
z_square = real*real + imag*imag;
if(z_square > threshold)
break;
else{
x = real;
y = imag;
}
}
y0 = y0 - delta;
}
x0 = x0 + delta;
}
(对应GMP实现):
GMP_init_calc()
GMP_reset_y0()
GMP_reset_x()
GMP_reset_y()
GMP_calc_real()
GMP_calc_imag()
GMP_calc_z_square()
if(GMP_cmp_threshold() > 0)
GMP_set_x_as_real()
GMP_set_y_as_imag()
GMP_update_y0()
GMP_update_x0()
GMP_clear()
GMP_init_calc()
GMP_reset_y0()
GMP_reset_x()
GMP_reset_y()
GMP_calc_real()
GMP_calc_imag()
GMP_calc_z_square()
if(GMP_cmp_threshold() > 0)
GMP_set_x_as_real()
GMP_set_y_as_imag()
GMP_update_y0()
GMP_update_x0()
GMP_clear()
这第3个程序对my floats类代码的唯一修改在于:在作近似计算时,要继续比较两种实现结果的一致性,需要对GMP的计算结果也作相应近似,那么必须在 我自己的float类作近似时有一个输出,告知GMP实现怎样作相应近似。这就是在truncate_floatII函数加了一个参数p_pos告诉GMP实现方面:我是在第几位 截断的,那么你也要在那一位作相应截断。
改变前后:
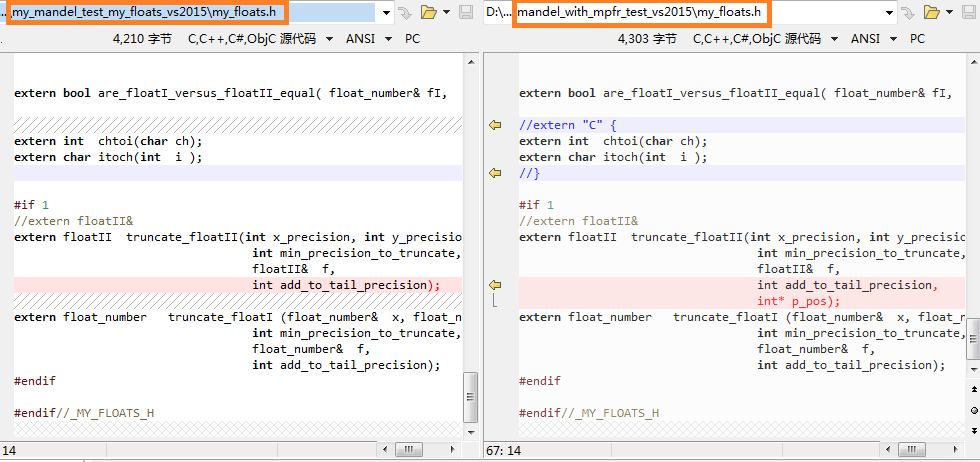
mandel_with_mpfr_test_vs2015\my_floats.h:
my_floats.cpp中作的相应改动下面即将看到。
extern floatII truncate_floatII(int x_precision, int y_precision, int delta_precision, int min_precision_to_truncate, floatII& f, int add_to_tail_precision, int* p_pos);
truncate_floatI目前未作改动,因为floatI和floatII的结果一致,我目前使用其中的一种就可以了,目前使用的是floatII。
加了GMP实现后,发现修正了my_floatI.cpp(my_floatII.cpp中同样)的一处(初级,:-))bug:
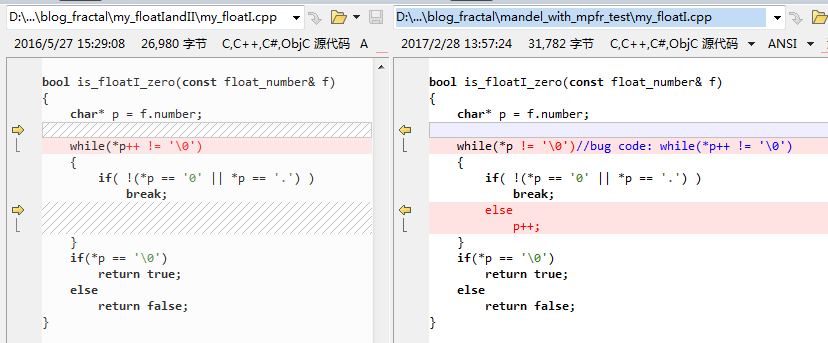
怎么又要作近似计算了呢?由于绝对精确的计算(不作任何近似)对存储小数的位数需求是随迭代次数幂指数式增长的,10次迭代以K计,20次迭代以M计, 30次迭代就以G计了。 此外这样计算在PC上迭代到第10次左右差不多千位乘千位数量级时算一个点已经感觉有点慢了。所以实际计算必须作一定的近似,比如让存储所需位数 随迭代线性增长。并考虑估量取得结果的速度。
目前我考虑的近似算法大致是这样的:
第(0)步:定一个精度提高位数要求,比如在原有精度上加16位;
第(1)步:定一个精度达到位数,需考虑(A)起始坐标精度;(B)坐标步进值精度;再加上第(0)步期望;(C)随迭代次数增加(?)
第(2)步:计算结果是否超出精度需求?若否,则不改变值;
第(3)步:若(2)是,计至小数点后精度位,然后:
(A)若前面已有有效数字,则向后加计最多如16位;
(B)若前面尚未有有效数字(全'0'),除非0值,向后找到第1位有效数字(非'0'值),然后向后加计最多如16位;
实现:(以floatII为例)((高亮行即上面所说该函数的改动添加))
mandel_with_mpfr_test_vs2015\my_floatII.cpp:
使用近似计算的代码所需改动:
floatII truncate_floatII(int x_precision, int y_precision, int delta_precision,
int min_precision_to_truncate,
floatII& f,
int add_to_tail_precision,
int* p_pos)
{
*p_pos = 0;
int truncate_part_len = 0;
int i;
//if(f.point_pos_r < min_precision_to_truncate)
// return f;
floatII approximation = f;
int max = x_precision ;
max = y_precision > max ? y_precision : max ;
max = delta_precision > max ? delta_precision : max ;
if(f.point_pos_r <= max)
return approximation;
max += add_to_tail_precision;
if(f.point_pos_r <= max)
return approximation;
else
truncate_part_len = f.point_pos_r - max;
max -= add_to_tail_precision;
//go to NO.`max' after '.' of f
/*
result (= x * y) ((precison of a by b )) :
(a) common case: (some non-'0' ahead)
0.02003004080509760000000001300xxxxxxxxxxxxxxxxx
(b) rare case: (all '0's ahead)
0.000000000000000000000000013000000050000xxxxxxxx
or 0.0000000000000000000000000130 (shorter vs. above)
*/
int len = strlen(f.digits);
int int_len = len - f.point_pos_r;
char* p = approximation.digits;
bool is_there_nonzero = false;
for(i = 0; i < (int_len + max); i++)
{
if(p[i] != '0')
{
is_there_nonzero = true;
break;
}
}
if(is_there_nonzero)
{
approximation.point_pos_r -= truncate_part_len;
int len2 = len - truncate_part_len;
memset(&p[len2], 0, truncate_part_len);
p[len2] = '\0'; //clear again ( redundant though)
*p_pos = len2 - int_len + 1;//*p_pos = &p[len2] - &p[int_len] + 1;
return approximation;// (.)
//531415
//0123456
// ^
}
else //TODO: to log and check this rare/corner case.
{
for(i = (int_len + max); i < len; i++)
{
if(p[i] != '0')
break;
}
if(i == len)
{
floatII result("0");
return result;
}
else
{
if( (len - i -1) <= add_to_tail_precision )
return approximation;
else
{
truncate_part_len = len - (i + 1 + add_to_tail_precision);
approximation.point_pos_r -= truncate_part_len;
memset(&p[i+1+add_to_tail_precision], 0, truncate_part_len);
*p_pos = i+1+add_to_tail_precision - int_len + 1;
return approximation;
}
}
}
}

其中GMP截断近似的实现:(以GMP_truncate_real()为例。GMP_truncate_imag()代码只是把"real"换成"imag"而已。)
mandel_with_mpfr_test_vs2015\mpfr_lib.c:
这个截断实现的原理是这样的: 由于程序中的分数都被设计为有限小数,不是无限小数,(更非无理数),对一等于形如小数53.1415926等等的
计算结果,让其乘以10的若干(将会是小数位数)次方直至得到整数(判断方法是分母为1),然后按照指定的截断位置,将整数字串该位置
及以后置为字符“0”,用此字串构造mpq_t,再除以10的相应次方。即完成了计算结果的截断。函数代码高亮第30行取得分母,第32行为待用乘数10,
34、36行可看到循环乘10并判断分母是否成了1。43行取得此时的分子,高亮第48行取得此时分子的字串。50-53行将此字串在截断位置后部置“0”。
55行构造新的GMP分数后,高亮第57、59行可见循环除以10的n次方。
void GMP_truncate_real(char* str_numerator, char* str_denominator,
char* str_gmp_mpfr, int* p_exp, int mpfr_precision,
int len, int trunc_pos)
{
mpz_t numerator;
mpz_t denominator;
mpq_t a;
mpfr_t f1, f2;
mpfr_exp_t exp;
mpz_init(numerator);
mpz_init(denominator);
mpq_init(a);
mpq_set(gmp_real_approx, gmp_real);
if(trunc_pos == 0)
{
//return;
}
else
{
int n;
char* str;
char* p;
mpz_set(denominator, mpq_denref(gmp_real_approx));
//gmp_printf("denominator is %Zd\n", denominator);
mpq_set_si(a, 10, 1);
n = 0;
while( mpz_cmp_si(denominator, 1) != 0)
{
mpq_mul(gmp_real_approx, gmp_real_approx, a);
//gmp_printf("%#040Qd\n", gmp_real_approx);
mpz_set(denominator, mpq_denref(gmp_real_approx));
n++;
}
//printf("\n multiplied by 10^ %d\n" , n);
mpz_set(numerator, mpq_numref(gmp_real_approx));
//gmp_printf("numerator is %Zd\n", numerator);
str = (char*)malloc(len+16); //some more space
memset(str, 0, len+16);//buggy: memset(str, 0, sizeof(str));
mpz_get_str(str, 10, numerator);
//printf("str got:%s\n", str);
p = str + strlen(str);
p -= (n-trunc_pos)+1; //53.1415926
while( *p != '\0')
*p++ = '0';
mpq_set_str(gmp_real_approx, str, 10);
mpq_canonicalize(gmp_real_approx);
while(n > 0)
{
mpq_div(gmp_real_approx, gmp_real_approx, a);
//gmp_printf("%#040Qd\n", approx);
n--;
}
free(str);
}
mpz_set(numerator, mpq_numref(gmp_real_approx));
mpz_get_str(str_numerator, 10, numerator);
mpz_set(denominator, mpq_denref(gmp_real_approx));
mpz_get_str(str_denominator, 10, denominator);
//for visualizing the string
mpfr_init2(f1, (mpfr_prec_t)mpfr_precision);
mpfr_init2(f2, (mpfr_prec_t)mpfr_precision);
mpfr_set_z(f1, numerator , MPFR_RNDZ);
mpfr_set_z(f2, denominator, MPFR_RNDZ);
mpfr_div(f1, f1, f2, MPFR_RNDZ);
mpfr_get_str(str_gmp_mpfr, &exp, 10, 0, f1, MPFR_RNDZ);
*p_exp =(int)exp;
mpfr_clear(f1);
mpfr_clear(f2);
mpz_clear(numerator);
mpz_clear(denominator);
mpq_clear(a);
}
讲了这么多,还没看到加法和乘法的代码。虽然这只是小学数学运算,这里还是大致看一下。虽然上面GMP显示了很强的功能,或许以后 更多计算用GMP(及MPFR)编程是更好的替代(因其可用分数,即无限循环小数,等等其他自己不具备的功能),在可用的地方多一种实现 并行可能更好。在不可用的地方只好用GMP了。
以floatII类的实现为例,floatI类的实现冗长一些,floatII类的简洁一点,算法是一样的。加法没太多好说的:
mandel_with_mpfr_test_vs2015\my_floatII.cpp:
高亮第7行开始,准备对齐小数点。20行得到小数点位置。24、25行把'0'字符补齐。27行同号,准备加,下面就是相加,记录进位值。
57行开始准备结果字符串,计算是从低到高即从右到左进行的,而计算结果字符串是从左到右表示。66行用字符串等构造fII类对象返回。
84行异号相减先比较绝对值大小。94行比较结果为相等,则返回0。104行准备用大的减小的。下面就是作相减、借位等。完成后
同样构造字符串后,149行构造fII类对象,完成。
floatII floatII::operator+ ( floatII& f2)
{
//TODO: 0?
int sign, pos;
//align point
floatII f1 = *this;
int int_len1 = strlen(f1.digits) - f1.point_pos_r;
int int_len2 = strlen(f2.digits) - f2.point_pos_r;
int frac_len1 = f1.point_pos_r;
int frac_len2 = f2.point_pos_r;
int max_int_len = int_len1 >= int_len2 ? int_len1 : int_len2 ;
int max_frac_len = frac_len1 >= frac_len2 ? frac_len1 : frac_len2;
floatII f1_old = f1;
floatII f2_old = f2;
//pos
pos = max_frac_len;
int len = max_int_len + max_frac_len;
char* s1 = f1.extend_zero2( max_int_len-int_len1, max_frac_len-frac_len1);
char* s2 = f2.extend_zero2( max_int_len-int_len2, max_frac_len-frac_len2);
if(f1.minus == f2.minus)
{
//minus assign
sign = f1.minus? -1 : +1;
int* carry = (int* )malloc( (len+1) *sizeof(int));
char* r = (char* )malloc( len );
memset(carry, 0, (len+1)*sizeof(int));
char* q = s1+len-1;
char* p = s2+len-1;
int m;
int k = 0;
while(q >= s1)
{
m = chtoi(*q) + chtoi(*p) + carry[k];
if(m >= 10)
{
carry[k+1] += 1;
r[k] = itoch(m-10);
}
else
{
r[k] = itoch(m);
}
p--;
q--;
k++;
}
char* str = (char* )malloc(len+1+1); //doesn't care if more
int i = 0;
int j;
if(carry[k] > 0)
str[i++] = itoch(carry[k]);
for(j = 0; j < len; j++)
str[i++] = r[len-1-j];
str[i] = '\0';
floatII str_result(str, sign, pos);
free(str); //? do it in destructor?
free(r);
free(carry);
free(s1);
free(s2);
return str_result;
}
else
{
//to decide sign
char* p = s1;
char* q = s2;
while(*p != '\0') // && *q != '\0'
{
if(chtoi(*p) != chtoi(*q))
break;
p++;
q++;
}
if(*p == '\0')
{
free(s1);
free(s2);
floatII f4("0");
if(MY_DEBUG) printf("they are equal,minus result is 0\n");
return f4;
}
else
{
bool t = chtoi(*p) > chtoi(*q) ? f1.minus : f2.minus;
sign = t? -1 : +1;
char* big = (*p > *q) ? s1 : s2;
char* small = (*p > *q) ? s2 : s1;
p = big + len-1;
q = small + len-1;
int* borrow = (int* )malloc( (len) *sizeof(int));
int n;
char* r = (char* )malloc( (len));
memset(borrow, 0, (len)*sizeof(int));
int k = 0;
while(p >= big)
{
if( (chtoi(*p) + borrow[k]) >= chtoi(*q))
{
n = chtoi(*p) + borrow[k] -chtoi(*q) ;
}
else
{
char* l = p-1;
while( chtoi(*l) == 0 )
{
*l = '9';
l--;
}
borrow[k] = 10;
*l -= 1;
n = chtoi(*p) + borrow[k] - chtoi(*q) ;
}
r[k] = itoch(n);
p--;
q--;
k++;
}
//TODO: to remove leading 0s in integer part
char* str = (char* )malloc(len+1);
int i = 0;
int j;
for(j = 0; j < len; j++)
str[i++] = r[len-1-j];
str[i] = '\0';
floatII str_result2(str, sign, pos);
free(str);
free(r);
free(borrow);
free(s1);
free(s2);
return str_result2;
}
}
}
乘法则用到两个重载*号的函数。两个类对象的相乘被转化成一个类对象与一个整数类型值相乘,即一个数与另一数的每一位相乘,然后把各个结果 作相应的小数点移位后相加。(比如对$f_{1}$ * $f_{2}$, $f_{2}$形如xyzwr.st0,结果则为 $$ \begin{aligned} result & = f_{1} * x * 10^m \space \space \space \space \space \space \text{(m=max_int_len-1)} \\ & + f_{1} * y * 10^{m-1} \\ & + f_{1} * z * 10^{m-2} \\ & + ... \\ & + f_{1} * t * 10^{-2} \\ & + f_{1} * 0 * 10^{-3} \space \space \space \space \space \space \text{(-3=-max_frac_len)} \end{aligned} $$ )。 故用了两个重载操作符的函数。
mandel_with_mpfr_test_vs2015\my_floatII.cpp:
高亮行即所述实现。第一个函数则与加法有类似的进位。
floatII floatII::operator* (int m) // 0<=m<=9
{
//TODO: 0?
int sign, pos;
floatII& f1 = *this;
sign = f1.minus? -1: +1; //does not care
//pos
pos = f1.point_pos_r; //doesn't change
int len = strlen(f1.digits);
char* s = f1.digits;
int* carry = (int* )malloc( (len+1) *sizeof(int));
char* r = (char* )malloc( (len));
memset(carry, 0, (len+1)*sizeof(int));
char* q = s+len-1;
int d;
int k = 0;
while(q >= s)
{
d = chtoi(*q) * m + carry[k];
if(d >= 10)
{
carry[k+1] += d/10;
d = d % 10;
}
r[k] = itoch(d);
q--;
k++;
}
//copied from add operation code part
char* str = (char* )malloc(len+1+1); //doesn't care if more
int i = 0;
int j;
if(carry[k] > 0)
str[i++] = itoch(carry[k]);
for(j = 0; j < len; j++)
str[i++] = r[len-1-j];
str[i] = '\0';
floatII str_result(str, sign, pos);
free(str); //? do it in destructor?
//copied from add operation code part -- end
free(r);
free(carry);
return str_result;
}
floatII floatII::operator* (const floatII& f2)
{
//TODO: 0?
int sign; // pos;
floatII& f1 = *this;
if(f1.minus == f2.minus)
sign = +1;
else
sign = -1;
char*p = f1.digits;
char*q = f2.digits; //(choose the shorter to be multiplier?)
floatII multi("0");
int len2 = strlen(f2.digits);
for(int i = 0; i < len2; i++)
{
floatII t1 = f1 * chtoi(q[i]);
floatII t2 = shift_floatII(t1, len2 - f2.point_pos_r - 1 - i);
multi = multi + t2;
}
multi.minus = (sign==-1)? true : false;
return multi;
}
floatII& shift_floatII (floatII& f, int m)
{
if(m > 0)
{
if(m >= f.point_pos_r)
{
f.extend_zero(0, m - f.point_pos_r);
f.point_pos_r = 0;
}
else
f.point_pos_r -= m;
}
else if(m < 0)
{
int int_len = strlen(f.digits) - f.point_pos_r;
if(-m >= int_len)
f.extend_zero(-m-int_len+1, 0);
f.point_pos_r += -m;
}
return f;
}
一直以来都只是c程序员,对c++知之甚少。这里进行数类的运算,使用c++,用重载运算符实现比较自然。使用GMP时,又感到用c库 比c++移植性好。
有一次发现第3个程序很快耗用内存太大,且不断增长。调试后发现少量把malloc/free改成new/delete的代码导致了这个问题,这还 不是内存泄漏,关闭进程后内存马上恢复了,但运行时这样的内存耗用下去马上程序就无法运行了,似乎new的内存delete后还没有 立即交还给OS,而free则立即交还了。由于程序要持续进行大量计算,不发生内存泄漏对程序是至关重要的。
自己实现下来用了少量代码取得了与GMP运算一致的结果,效果还不错。GMP用分数形式,比我用小数形式大大拓展了运算范围,当然, 算法更复杂了。我此处的算法只有乘法和加法,只适用于计算Mandelbrot集(不知是否适用于计算Julia集),其他分形计算不一定够用。
除了Win/VC,也准备在Linux/GTK上实现。
本想能在ReactOS上发布程序最好。但我在虚拟机上试用了ReactOS,其兼容性和稳定性都还不行。 ……
(附及:MPFR的精度是指二进制精度,这与我的float小数实现用的10进制精度匹配的话可能有点问题。)
试图建立一个Mandelbrot集的图库,附上所写的PHP前端和c程序后端, 参看PDF电子书 及其制作shell等。但由于所需计算性能极高,要更精确计算还不够实用。