(The gallery is shown on this page.)
There is a program named "backfract" on the web(Its link: Backfract. Its author also released a Go game front end named "cgoban", which can be found by Baidu search engine while backfract can't). It can render Mandelbrot set fractals. This program can display various areas of Mandelbrot set in full screen automatically and the visual effect is very good(Here I list some of them:backfract examples). It runs on _unix/X. On its homepage it is said that the program "randomly" selects "interesting" areas to display, but does not purely zoom in, sometimes it zooms in, sometimes it zooms out next. There are also some videos on the web alleged to be able to zoom in by a factor of 10's power "N". Usually they finish playing back in several minutes. I consider whether I myself can zoom it in infinitely, at least as most as possible.
In mathematics, there are two kinds of definitions for Mandelbrot set. In the book Chaos Fractals And The Applications and the book The Computer Images of Fractals And Its Applications, roughly it speaks like this: The Mandelbrot set is related to another kind of set: Julia set. Notate the quadratic mapping with point c as its parameter as $ f_{c} = z^2 + c $ , for any point c on the complex plane there is a corresponding Julia set. Some c points' corresponding Julia sets are connected while others are not, by this, there is below definition for Mandelbrot set:
Mandelbrot set M is a set of parameters c that each makes the Julia set corresponding to the $f_{c}$ mapping of it a connected set, i.e.
$$ \begin{aligned} M = \left \{ c \in \mathbb{C} \space \space | \space \space J(f_{c}) \text{ is a connected set} \right \} \end{aligned} $$ If we plot every c that is accompanied by a connected corresponding Julia set on the complex plane, then the set of c's is M set fractal. This definition is not good for computer processing, luckily, another equivalent definition of Mandelbrot set has been proved in mathematics: $$ \begin{aligned} M = \left \{ c \in \mathbb{C} \space \space | \space \space \lim_{n \to \infty} Z_{n} \nrightarrow \infty \right \} \end{aligned} $$ in which, $$ \begin{aligned} Z_{0} & = 0 \\ Z_{n+1} & = Z_{n}^2 + c \end{aligned} $$ This web page (The Mandelbrot Set) talked about handling of some problems met in the actual plotting:(1) Judgement of infinity
In mathematics, it can be proved that the Mandelbrot set is fully enclosed inside the closed circle which takes the origin as its center and is of radius 2, that is: $$ \begin{aligned} M \subset \left \{ c \in \mathbb{C} \space \space | \space \space \left| c \right| \leqslant 2 \right \} \end{aligned} $$ So if one intermediate result of the iteration is of a modulus lager than 2, then it will definitely go to infinity if the iteration continues. So we use modulus 2 as a threshold value.
(2) Times of iteration
The author of the above web page gave an example applying 50 times. But I ever met the case of different results between 50 times iteration and 200 or 1000 times iteration. So I haven't been clear about the mathematical basis of this question yet.
(3) Coloring
In fact the Mandelbrot set is only of the form of the middle (black) part. All the points outside of it do not belong to Mandelbrot set. It is not very visually appealing by simply plotting a black and white image marking whether each point belongs to Mandelbrot set or not. The various colorful details we have usually seen depend on coloring. One common method is to select the color according to the modulo arithmetic of iteration times of the "escaped" point. (One other method is similar to contour line plotting, which is not used here.) But the effect of a rather simple coloring cannot compare with that produced by a program like backfract.
(The pseudo-code that calculates whether the point of coordinate $(i,j)$ in the drawing window belongs to the M set or not and then colors it):
$x_{0} = $ left_coord + delta* $i$;
$y_{0} = $ above_coord - delta* $j$;
$ x = x_{0}$ ; // or $ x = 0 $
$ y = y_{0}$ ; // or $ y = 0 $
int $ k = 0 $ ;
while( $ k \lt $ MAX_ITERATION )
{
real = $ x^2 - y^2 + x_{0} $;
imag = $ 2xy + y_{0} $ ;
$ {|z|}^2 = $ real*real + imag*imag ;
if( $ {|z|}^2 \gt 4 $ )
break;
else{ $ x = $ real; $ y = $ imag; }
$k$ ++;
}
if( $ k \lt $ MAX_ITERATION )
SetPixel(hdc, $i$, $j$ , colors[ $k$ %50]) ;
else
SetPixel(hdc, $i$, $j$ , RGB(0, 0, 0)) ;
$x_{0} = $ left_coord + delta* $i$;
$y_{0} = $ above_coord - delta* $j$;
$ x = x_{0}$ ; // or $ x = 0 $
$ y = y_{0}$ ; // or $ y = 0 $
int $ k = 0 $ ;
while( $ k \lt $ MAX_ITERATION )
{
real = $ x^2 - y^2 + x_{0} $;
imag = $ 2xy + y_{0} $ ;
$ {|z|}^2 = $ real*real + imag*imag ;
if( $ {|z|}^2 \gt 4 $ )
break;
else{ $ x = $ real; $ y = $ imag; }
$k$ ++;
}
if( $ k \lt $ MAX_ITERATION )
SetPixel(hdc, $i$, $j$ , colors[ $k$ %50]) ;
else
SetPixel(hdc, $i$, $j$ , RGB(0, 0, 0)) ;
The floating point computation got the IEEE 754 standard, and books on computer architecture generally will talk about it. There are also books such as Floating Point Computation Programming Principles Implementation And Application by Chun-Gen Liu (in Chinese) that illustrate it. And there is a famous article on the web: What Every Computer Scientist Should Know About Floating-Point Arithmetic.
This article got three related programs:
The first one uses machine float, that is, the double data type in c/c++ and plots Mandelbrot set in VC++. Besides, it lets the user select an area to zoom in various parts by "rubber band";
The second one adds into the above code my class implementation for floating-point number, and compare the result to that of the above machine float. But I haven't modified and finished the function of "rubber band" yet;
The third one doesn't take a GUI, it purely compare the computation result of my floating-point implementation with that of GMP fraction implementation so to check their consistency.
The three programs were developed under WinXP + VC++6 on VMWare3 at the very beginning. Later they are updated to Win7 + vs2015(MFC installed) on VMWare6, with minor modifications. Both versions are provided here:
VC++6 version vs2015 version
(The code had not been cleaned up, :-(. )
The 1st program
(1)double type implementationThis code part of operation is nearly the same as the above pseudo-code:
my_mandel_test_3(machine_float)\my_mandel_testView.cpp:
for(i = 0; i < w; i++)
{
for(j = 0; j < h; j++)
{
BOOL b_is_boundary = FALSE;
if(delta_w > delta_h)
{
if( j == (int)( (h*delta - (old_above_coordinate- \
old_below_coordinate))/(2*delta) )
|| j == ( h-(int)( (h*delta - (old_above_coordinate- \
old_below_coordinate))/(2*delta) ) )
)
b_is_boundary = TRUE;
}
else
{
if( i == (int)( (w*delta - (old_right_coordinate- \
old_left_coordinate))/(2*delta) )
|| i == ( w-(int)( (w*delta - (old_right_coordinate- \
old_left_coordinate))/(2*delta) ) )
)
b_is_boundary = TRUE;
}
double x0 = left_coordinate + delta * (double)i;
double y0 = above_coordinate - delta * (double)j;
double x = x0;
double y = y0;
int k = 0;
#define MAX_ITERATION 1000
while(k < MAX_ITERATION)
{
double real_part = x*x-y*y+x0;
double imaginary_part = 2*x*y+y0;
double z_abs_square = real_part*real_part + imaginary_part*imaginary_part;
if(z_abs_square > 4.0)
{
break;
}
else
{
x = real_part;
y = imaginary_part;
}
k++;
}
if(k < MAX_ITERATION)
{
//unsigned long colors[16] =
unsigned long colors[50] =
{
RGB(0xDE , 0xB8 , 0x87),
...
RGB(0x19 , 0x19 , 0x70 )
};
//SetPixel(hdc, i, j , colors[k%16]);
SetPixel(hdc, i, j , colors[k%50]);
if(b_is_boundary)
SetPixel(hdc, i, j , RGB(255, 255, 255));
}
else
{
SetPixel(hdc, i, j , RGB(0, 0, 0));
if(b_is_boundary)
SetPixel(hdc, i, j , RGB(255, 255, 255));
}
}
}
Its running result is like below:(To save the space, below pictures displayed are those zoomed out by the browser. To browse them in their original size, click this link. Or you can right click below pictures and save them to your local storage for watching.)
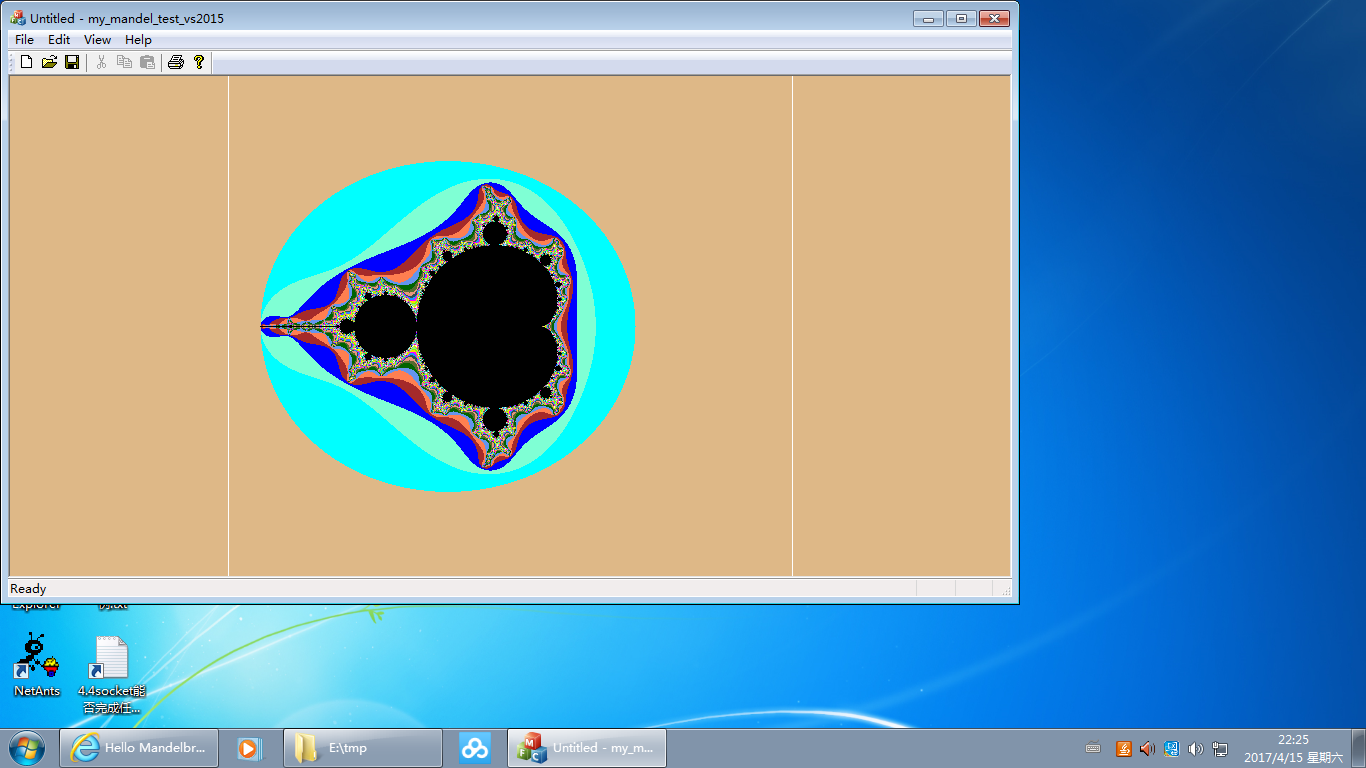
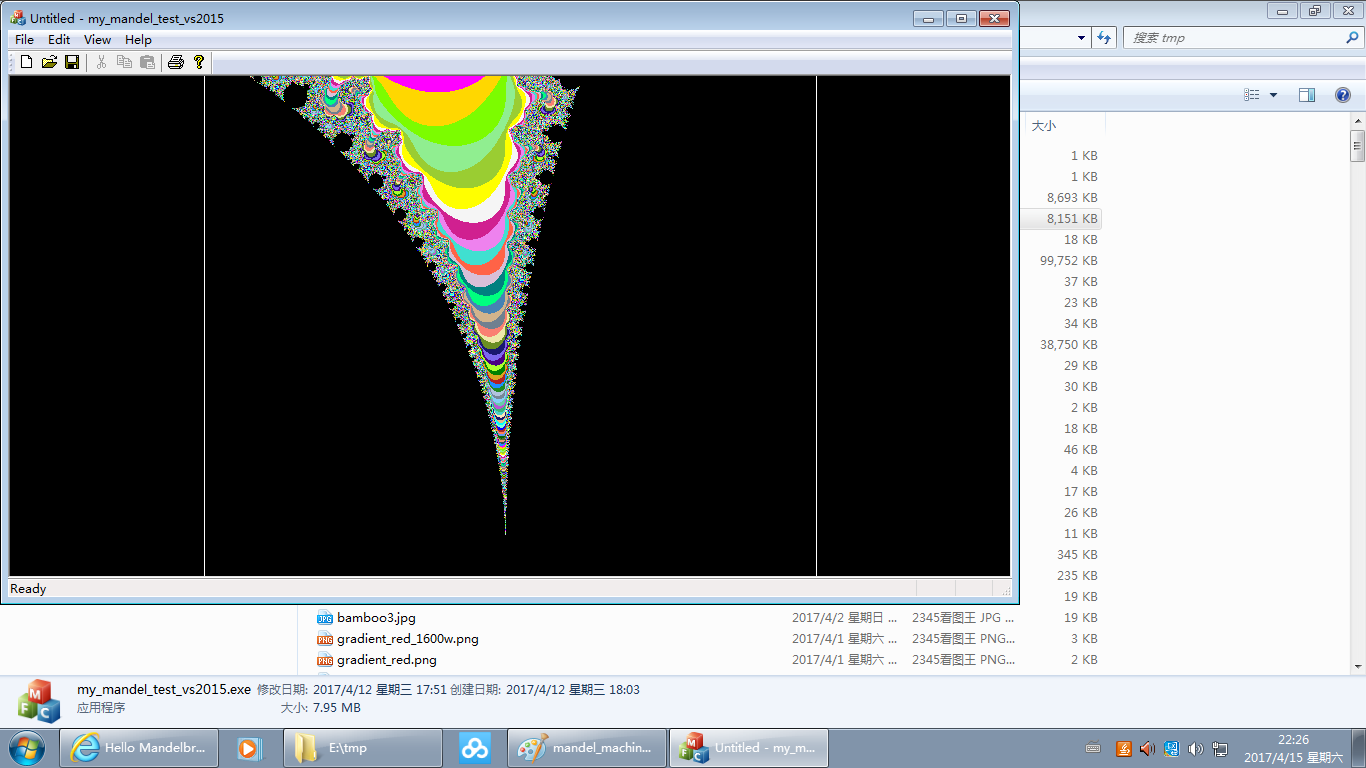
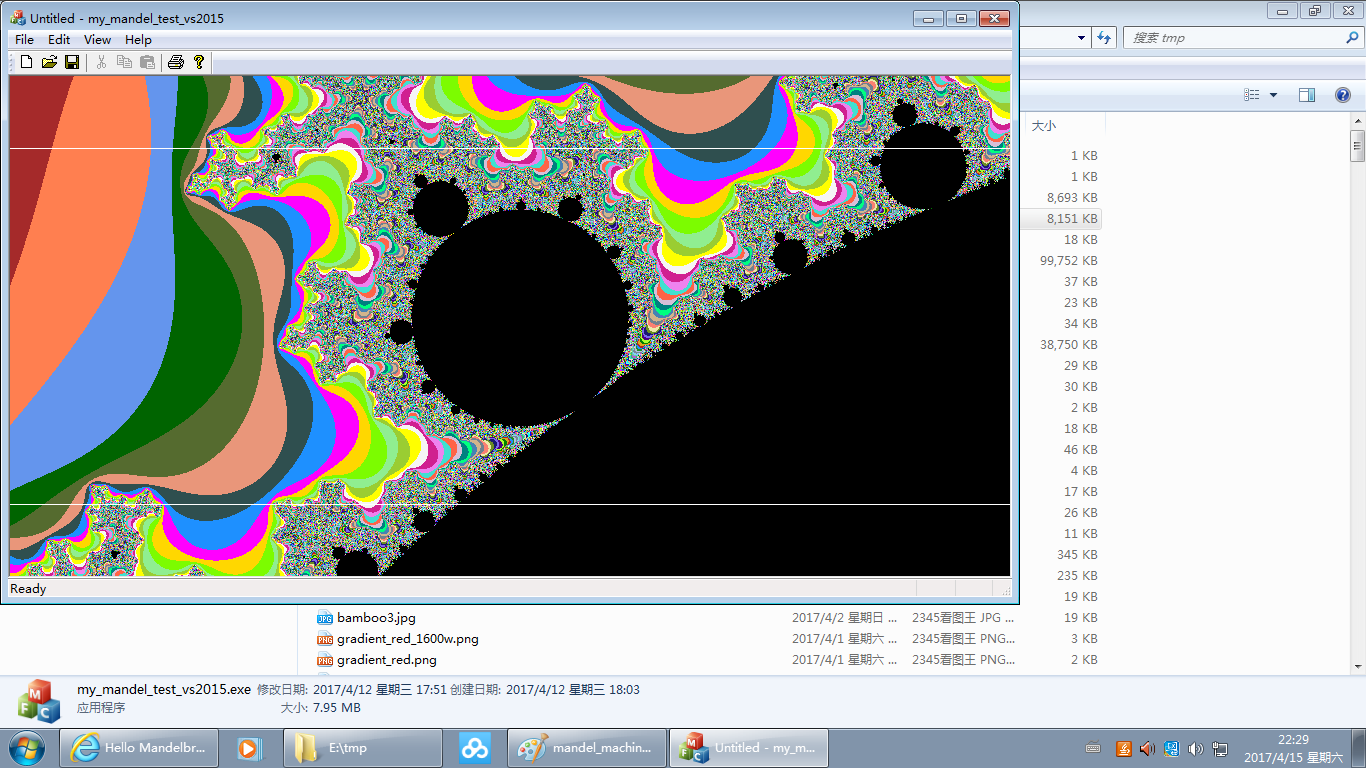
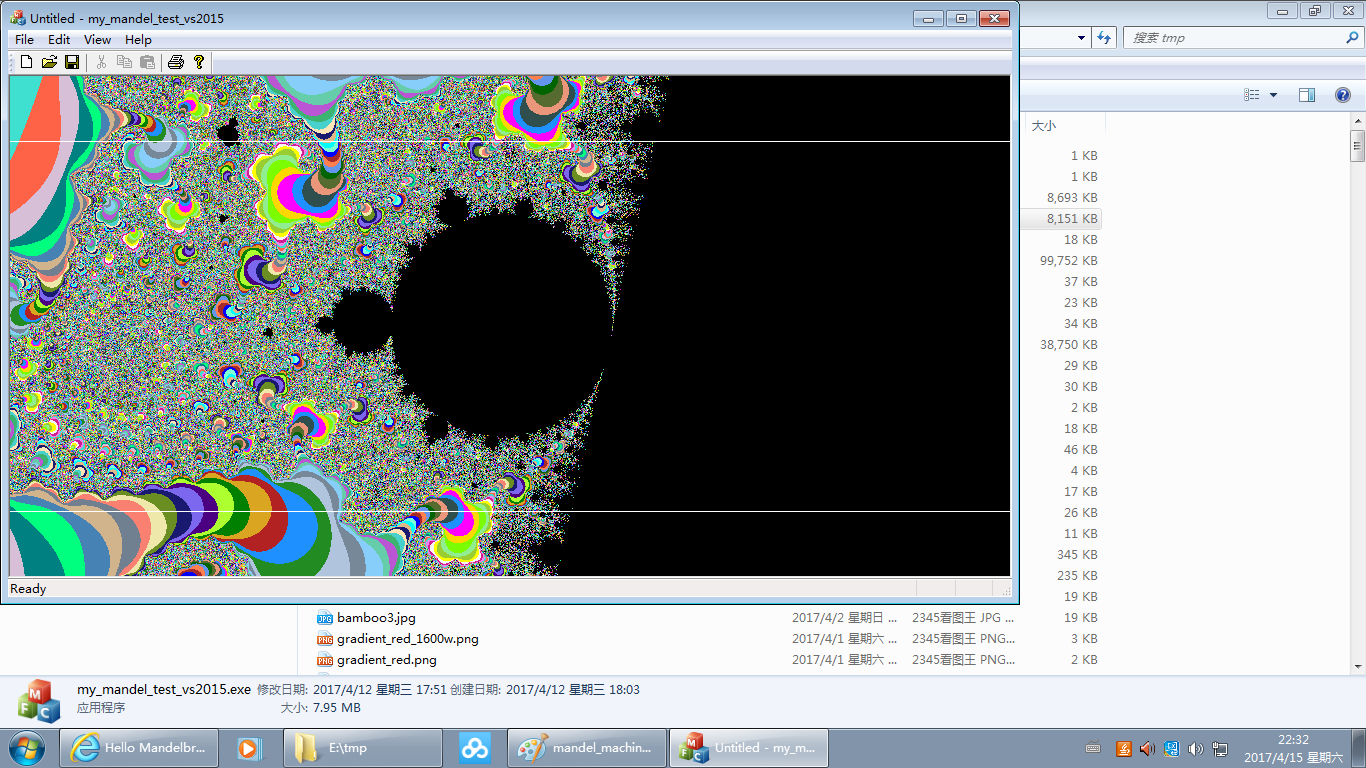
The proportion of the area selected to zoom in by the user is very likely not the same as that of the drawing window. So I make some extension to it to adapt to the drawing window so to make every pixel point inside the drawing window being plotted. The inner part within the two white lines in each of the above images is the area selected by the user(the visual effect maybe is poor for small pictures, you can turn to the original ones), which may appear too flat or too high for the drawing window. The judgement processing of "b_is_boundary" in the above code is for this reason.
(Two intermediate text files draw_coordinates.txt and arguments.txt are generated after you run the program. You need to delete them manually before the next run.)
The machine double float is of a binary precision of 53 bits, roughly 16 decimal places of accuracy. The starting horizontal and vertical coordinates are both of a magnitude of about (-2,2). If each time the dimension of the selected area for zooming in is about one tenth of that of the original image, we may find that after about 16 times of selection the image went "mosaic". Bare 16 times, this is far less than infinitely zooming it in. Besides, we will see behind that after about 40 times of iteration, the log already shows that the accumulation of error from machine float operation leads to obvious fault.
The 2nd program
(2) my floating-point class implementationSince the calculation is only concerned with addition and multiplication operation, we should be able to do completely accurate calculation for the terminating decimals. The arithmetic taught in primary school should suffice. In order that we only need to compute terminating decimals, we only use starting coordinates and step values with finite fraction part. The latter is achieved by specifying the width and height of the drawing window as some particular values such as 500/512/800/1000/1024 so that the gap value between two pixel points is also a simple terminating decimal.
That's why I modified the code in View.cpp to support only these particular values.
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.cpp:
if (!(w == 200 || w == 250 || w == 400 || w == 500
|| w == 800 || w == 1000 /*|| w == 1024*/)
|| !(h == 200 || h == 250 || h == 400 || h == 500
|| h == 800 || h == 1000 /*|| h == 1024*/)
)
{
AfxMessageBox(L"width and height not supported");
return;
}
char* one_w_strI = (w == 200) ? "0.005" : (
w == 250 ? "0.004" : (
w == 400 ? "0.0025" : (
w == 500 ? "0.002" : (
w == 800 ? "0.00125" : (
w == 1000 ? "0.001" : ("error characters")
)
)
)
)
);
char* one_h_strI = (h == 200) ? "0.005" : (
...
The reader maybe still needs to modify the code in View.h, setting the width and height of the program window that suit your display area and meet the above specification.
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.h:
#define DEFAULT_CLIENT_AREA_WIDTH 500//1000 #define DEFAULT_CLIENT_AREA_HEIGHT 250// 800
The starting coordinates are: x: -2.5 to 2.5 , y: -2.0 to 2.0 :
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.h:
fI fI_left_coord("-2.25");
fI fI_right_coord("2.25");
fI fI_above_coord("2.0");
fI fI_below_coord("-2.0");
Three new files(my_floats.h, my_floatI.cpp and my_floatII.cpp) that implement my floating-point class and several helper functions were added. (Sometimes it reported error when I built the project under VC6 but passed after I re-added those files to the project. And it could never pass building under vs2015, reporting re-definitions found in nafxcwd.lib/uafxcwd.lib and libcmtd.lib. To solve this issue, one maybe need to adjust the project. First, ignore these two libraries in the "input" entry of the "link" option of the project; then, add these two libraries as per the above order to the "Other library dependencies".) Two different kinds of data structure for floating-point were implemented successively. Because it occured to me that the latter new one maybe would be better than the former one that had been implemented, I did them one after another.
The first implementation:
my_floats.h:
class float_number{
public:
bool minus;
char* number; //in absolute value form
int point_pos;
...
};
The second implementation:
my_floats.h:
class floatII{
public:
bool minus; //with '-' sign?
char* digits; //no '.' inside
int point_pos_r; //counting from the right side
...
};
Sometimes abridged as:
my_mandel_test_my_floats_vs2015\my_mandel_test_my_floats_vs2015View.cpp:
Both classes use seperated member "minus" to represent whether the floating-point number is positive or negative, so the digits string of
the number(member "number" or "digits") all goes without symbol of sign. The first difference between the two classes is that
the decimal point was reserved in the digits string in the previous class implemented, but it vanishes in the latter class.
The second difference is the mark of the place of the decimal point, in the previous class it is counted from left to right(point_pos),
in the latter class, however, is counted from right to left(point_pos_r). Thus the implementation code of the latter class
is more concise. The computation results of these two implementations can be compared to each other to verify the code. This is
a second way for verification. But the cores of the algorithm of these two classes are the same, so probably its function
for verification is limited. A complete verification relies on the third program below which implements the contrast of the computation results
herein to that of the GMP calculation. That is a third way for verification, also can be said as the real verification.
(A first way for verification is a rather local one, it only verifies addition, i.e. do a reverse operation back after an addition
finishes and see if the result can be restored correctly. This way is little used.)
typedef float_number fI; typedef floatII fII;
Floating-point classes being accomplished, take fI class implementation as an example, the code is changed to roughly like this:(The actual code will interleave a little because of the need for result comparison. The example here is of an early version of code.)
my_mandel_test_my_floats_0\my_mandel_testView.cpp:
fI fI_left_coord ("-2.25");
fI fI_right_coord( "2.25");
fI fI_above_coord( "2.0" );
fI fI_below_coord("-2.0" );
fI delta_wI, delta_hI, deltaI;
#if 1
fI w_factorI(one_w_strI);
fI h_factorI(one_h_strI);
delta_wI = (fI_right_coord - fI_left_coord ) * w_factorI;
delta_hI = (fI_above_coord - fI_below_coord) * h_factorI;
if(delta_wI > delta_hI)
deltaI = delta_wI;
else
deltaI = delta_hI;
#endif
#if 1
fI x0I(fI_left_coord );
fI y0I(fI_above_coord);
fI aI("2");
fI threshold("4.0");
#endif
#if 1
for(i = 0; i < w; i++)
{
y0I = fI_above_coord;
for(j = 0; j < h; j++)
{
fI xI("0");
fI yI("0");
int k = 0;
#define MAX_ITERATION 10//20//100
while(k < MAX_ITERATION)
{
fI real_part = xI*xI-yI*yI+x0I;
fI imaginary_part = aI*xI*yI +y0I;
fI z_abs_square = real_part*real_part + imaginary_part*imaginary_part;
if(z_abs_square > threshold)
{
break;
}
else
{
xI = real_part;
yI = imaginary_part;
}
k++;
}
if(k < MAX_ITERATION)
{
SetPixel(hdc, i, j , colors[k%50]);
}
else
{
SetPixel(hdc, i, j , RGB(0, 0, 0));
}
y0I = y0I - deltaI;
}
x0I = x0I + deltaI;
}
#endif
The fII class code is similar, basically it just changes "I" to "II" or appends a suffix "II".
The illustrations showing the running result:(Now one can see the program is drawing the pixels of the screen one by one. Below are two images, an early one on the left and a late one on the right.)
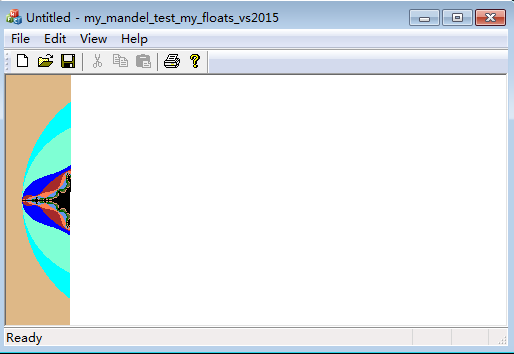
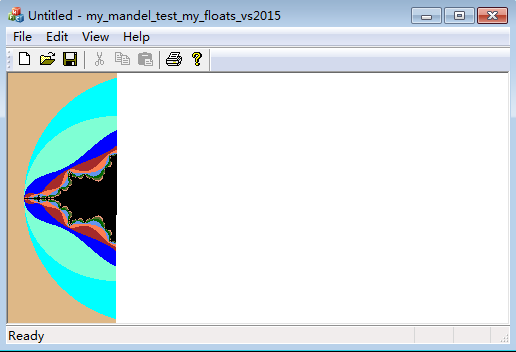
Below we give a graphic illustration for the log file:
(The blue wireframes orderly marked the coordinates in the window, the coordinates in the complex plane(the strings are in two kinds of form: fI form and fII form), iteration order, total iteration times when the computation loop ends.)
(The red wireframes orderly marked the real part, the imaginary part and the square of the modulus of z computed using machine floating-point.)
(The green wireframes orderly marked the real part, the imaginary part and (the high-precision approximation value of) the square of the modulus of z computed using my class code(fI and fII, which have the same result values).)
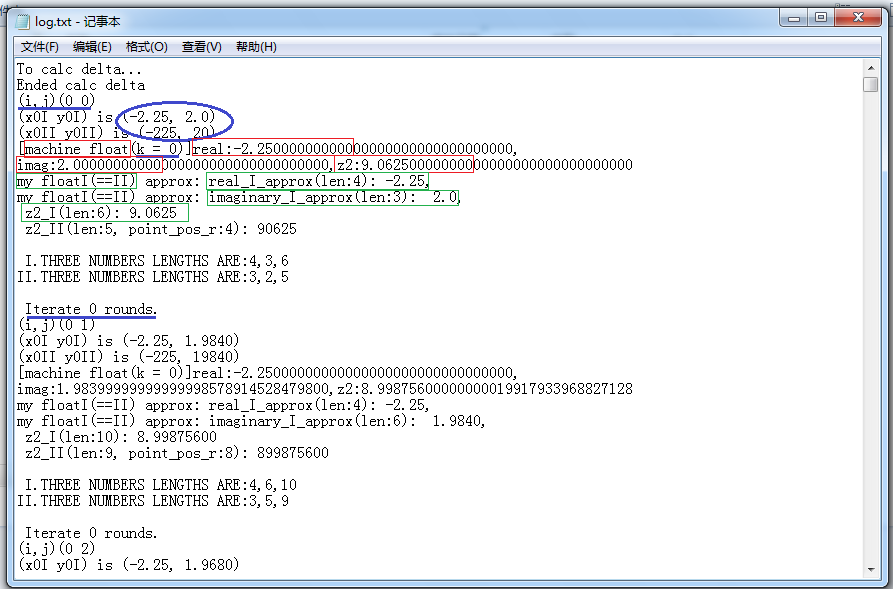
It can be seen that the point that lies at (0 0) exits the loop in just one time of iteration, which is outside of M set. It then
goes to compute the next point (0 1).
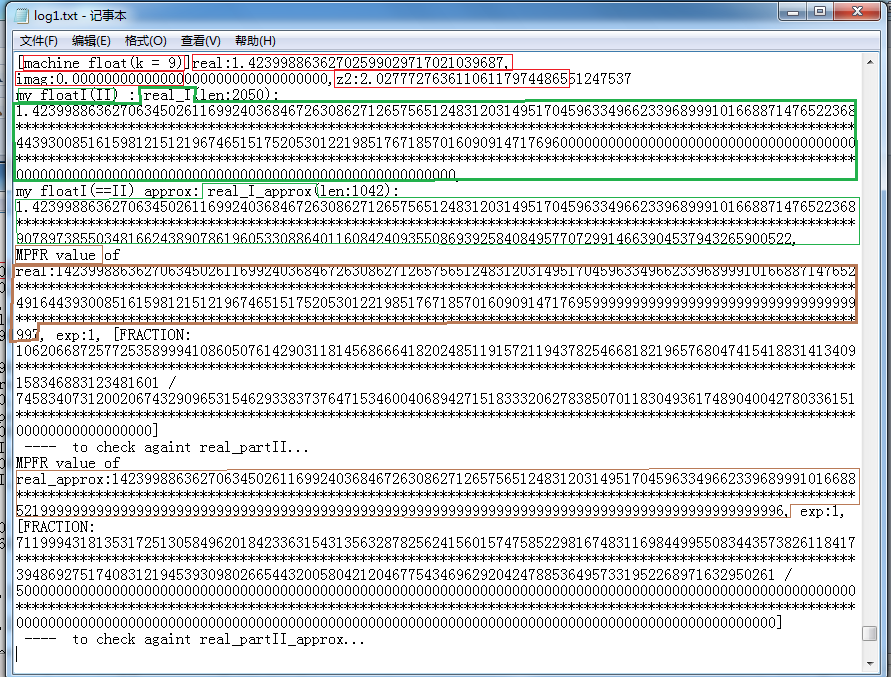
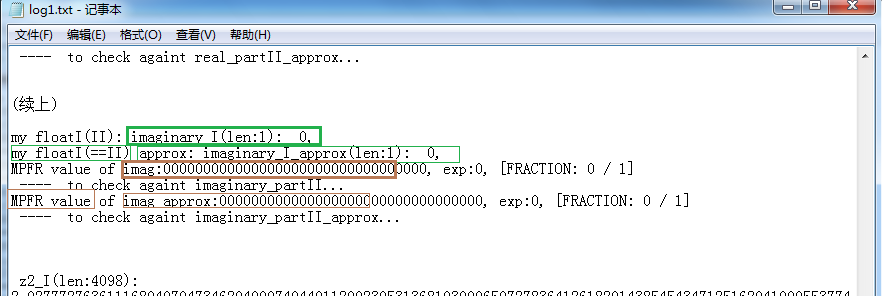
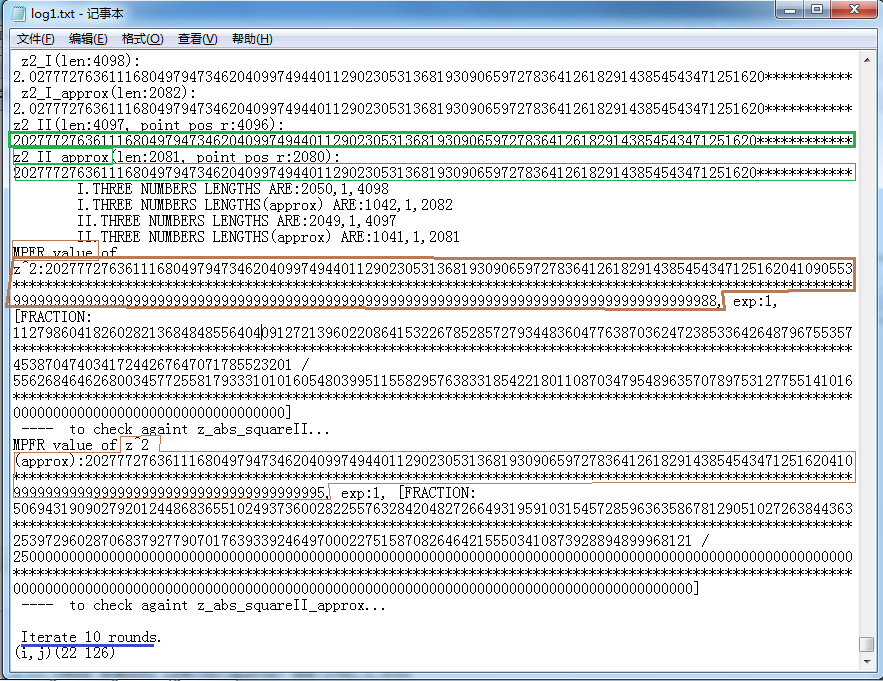
Below we give one more example, the pixel point (16 125):
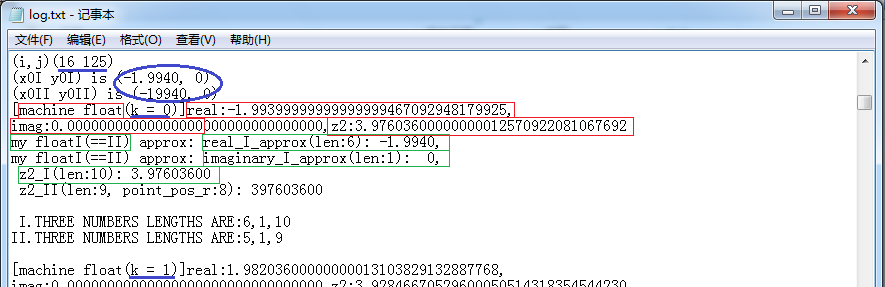
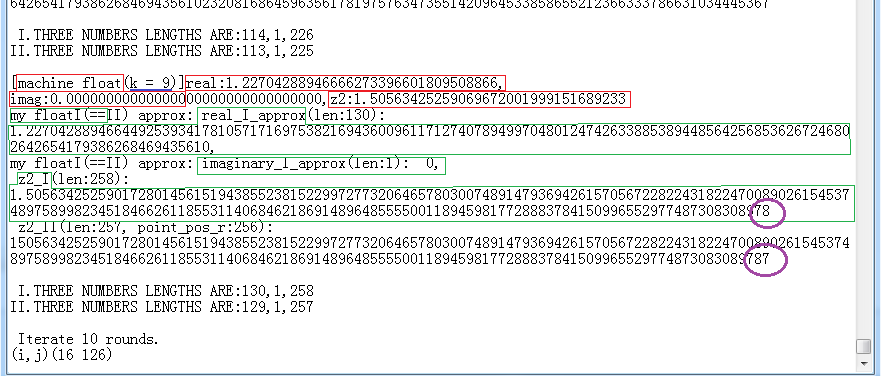
(The contents marked by the purple wireframes at the end of the digit strings are different. This is not because the computation results are different. It is because that I only print up to 200 digits at most while the length of the string of the result value is larger than 200. The string in fI form got one more character, i.e. the decimal point '.' than that string in fII form, so its output got one less digit than the latter.)
It can be seen that the point lies at (16 125) is on the real axis and belongs to M set. So the iteration reached the maximum(here it is 10 times) and the value still didn't exceed the threshold. The code did no more calculation and went to next point (16 126).
It brings dense computation to conduct accurate calculation using my floating-point classes. In my code, the calculation code was simply placed inside the OnDraw() function, this resulted in that the program didn't respond to external messages. This no responding maybe doesn't matter much under Win XP yet, one can still see the program is still drawing on the screen one pixel by one pixel. But it becomes worse under Win 7: the program draws no more than a few pixels and then just displays "The program does not respond".
To avoid blocking message loop because of dense computation(Blocking message loop is not blocking process. OnDraw() is located in the main thread, dense computation inside of it will make the main thread run inside this function for a long time, and will delay the message loop(that implemented by MFC itself)), I need to either start another worker thread to compute ,or insert message handler loop code by myself into the dense computation. Here the latter method is used. But it met a problem when closing the window, the process doesn't exit and the OnDraw() is still running, so I can only add some handling in the OnDestroy() function in View class.
Being able to conduct accurate calculation using my floating-foint classes, it may be found that how the error from machine floating-point (i.e. double type) computation which is intrinsically approximate could accumulate. Below is the log example. (log files for download(Below extracted part is at the very end of the log file.))
(Since the iteration times is large, here it is the approximation in some certain precision of the calculated reult using my floating-point class that is compared to the calculated result using machine floating-point, of course, this precision is highly better than that of double type.)
Here it is the iteration of the point of coordinate (16, 125) that is logged:
(The value inside the red rectangle is machine floating-point result. The value inside the green rectangle
is my floating-point result. )
(P.S. In the path showed in below image, the name of the directory that log.txt lies in is in Chinese, which means "logs comparison that shows machine floating-point got obvious error after more than 40 times of iteration"; see the sub-directory name of the above log file for download.)
(P.S. In the path showed in below image, the name of the directory that log.txt lies in is in Chinese, which means "logs comparison that shows machine floating-point got obvious error after more than 40 times of iteration"; see the sub-directory name of the above log file for download.)
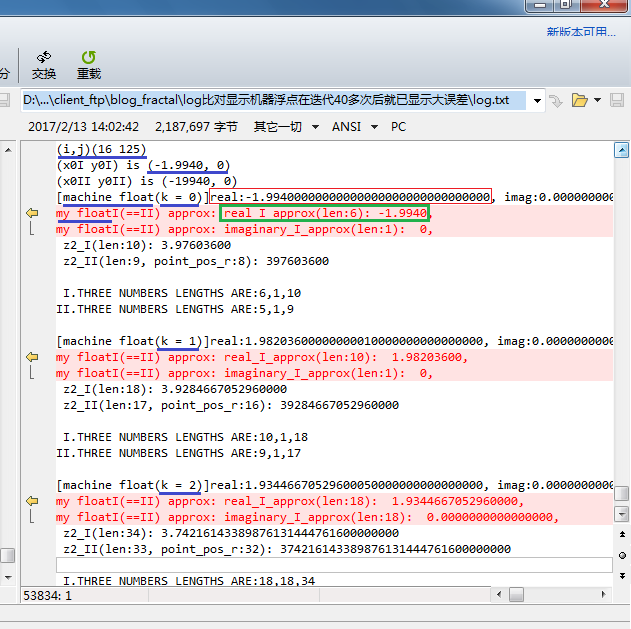
When k = 40, the difference isn't large;
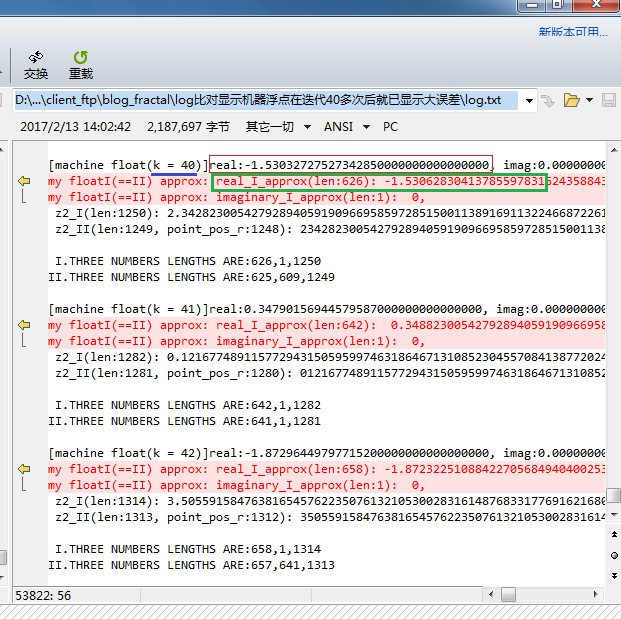
When k = 47, there is difference at the first decimal place;
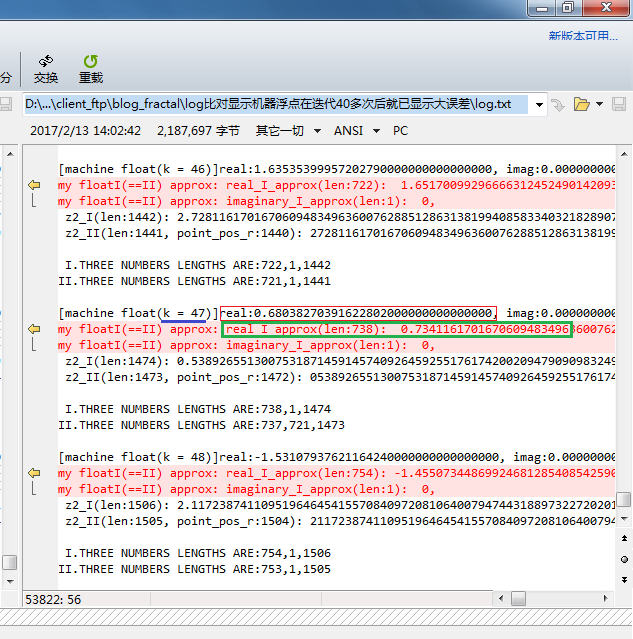
When k = 52, already we cannot think they are close ;
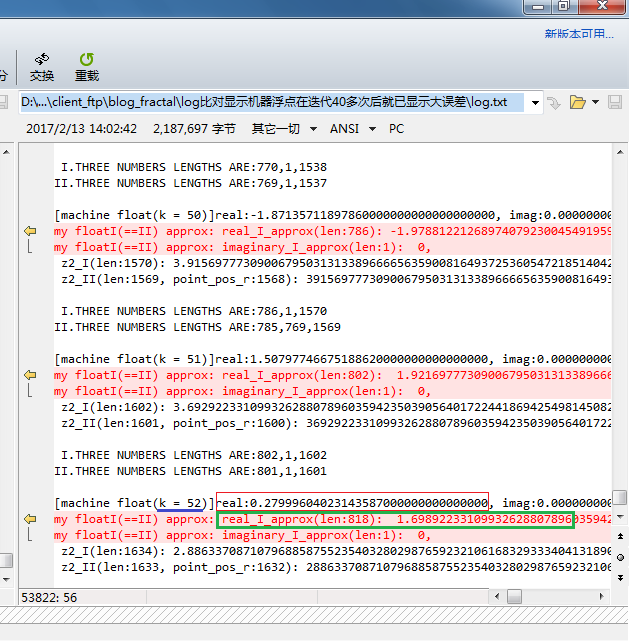
Since k = 53, the results might have got different plus or minus signs!
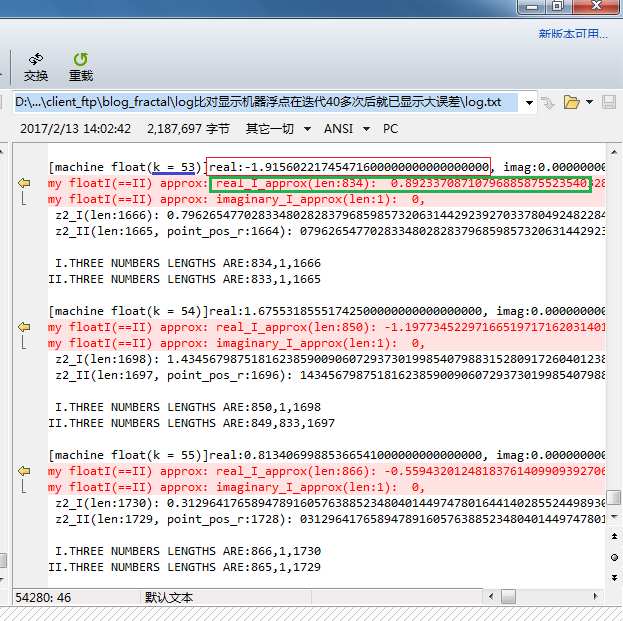
(It seems that "backfract" uses "long double" type instead of "double". Still this is too little.)
The function to select a region to zoom in is not implemented in this version of code. Besides, the zooming-in of M set is endless, I need to consider how to zoom it in on earth. Manual selection? Or automatic selection? How should I present the image patterns of the M set?
The 3rd program
(3) GMP implementationGMP library is the GNU "big number" library. The GMP library I used was built under MinGW on WinXP on VMWare3, it can then be directly linked into the applications developed under VC++6, along with some more libraries of MinGW and Windows. When I upgrade/update my program on Win 7+vs2015 on VMWare6, the library itself is still usable, only that the fprintf() function cannot be used for the reason of libmsvcrt.a of MinGW. So I replaced all the "fprintf"s with "fwrite"s. For running, some VC libraries from VS and some libraries from MS SDK that are prompted to be in need are added.
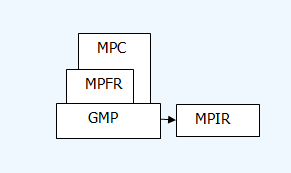
GNU big number libraries are composed of GMP, MPFR, MPC. GMP is big integer and fraction number library. It also included function part for floating-point operation but that now is replaced by MPFR(said in GMP manual). MPFR is arbitrary precision big floating-point number library, it is based on GMP. MPC is big complex number library and it is based on the former two libraries. (It is interesting that GCC building is dependent on these libraries.) Besides, There is another library MPIR branching from GMP. It is said that one of MPIR's goals is to become a big number library that can be built with VS under Windows because GMP cannot. Here MPIR is not used. I ever thought I would need MPFR to realize the function needed, thus "mpfr" is used in the file name ("mandel_with_mpfr_test") but later I found that mere the fraction part of GMP library could suffice. And the latter calculates in absolute precision, not limited to the arbitrary precision of the former. Yet the file names are not modified. Actually nearly my whole program has nothing to do with MPFR except only at one place I use it to print a log record.
I installed a MinGW+MSYS offline-install package downloaded from the web on WinXP on VMWare. As the manual and "configure" help guided, I configured and compiled GMP and MPFR(The source package of MPFR got a file(INSTALL) talking about three ways for building it under Windows(MinGW, Cygwin and vs2015)). There is nothing peculiar. But the library to be built can only be specified either as static or as shared/dynamic each time. I just built static ones. The two static libraries(libgmp.a and libmpfr.a) obtained can directly be used by VC++6 and vs2015:
mandel_with_mpfr_test_vs2015\mpfr_inc.h:
All other lib*.a files are MinGW libraries that are needed when building the program. Besides, to run the program one need
libgcc_s_dw2-1.dll of MinGW and some dlls of Windows.
#pragma comment(lib, "libmpfr.a") #pragma comment(lib, "libgmp.a") #pragma comment(lib, "libgcc.a") #pragma comment(lib, "libgcc_s.a") #pragma comment(lib, "libmingwex.a") #pragma comment(lib, "libmsvcrt.a")
GMP is implemented in c. It got a C++ wrapper library that could be configured and built. But the manual said that this c++ library generally can only be used by the application built with the same (c++) compiler. In development I found that I must use c compiler instead of c++ compiler to compile one source file that includes gmp.h, so my mpfr_lib.c has to be .c file instead of .cpp file.
Link order is required for MPFR library, first libmpfr.a, then libgmp.a. And the manual says that in some cases one must specify /MD option for the Windows cl compiler to build VC++ application using GMP library.
(There is an open source project on fractals named "FractalNow". It got MPFR computation joined into its code since version 8.0. This project is dependent on Qt. I built this project under both Ubuntu and WinXP MinGW. It got a debian package in the Ubuntu repository and was rather easy for building. On Windows, however, the Qt4.8 it depends on requires GCC4.4 for building. I could only search for and download one MinGW package with GCC4.4, then copy the earlier MSYS directory, moreover, download the "pthreads-w32" package, thus accomplished its building.)
Running effect:
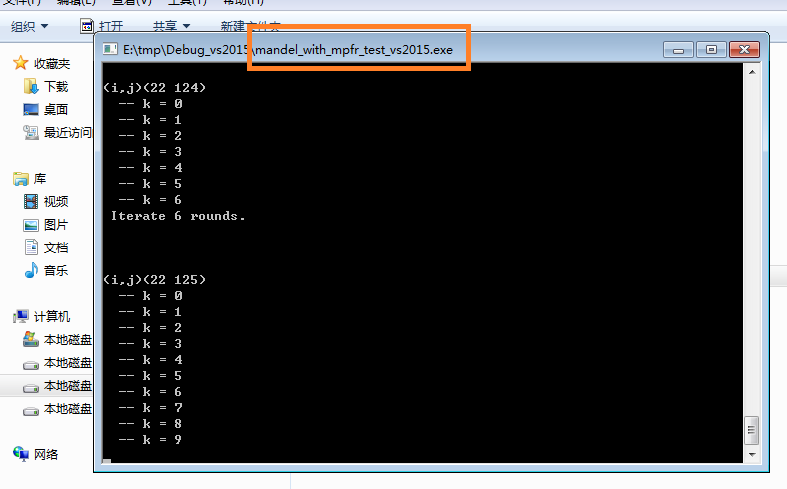
As to the log file, it got some more contents, mainly the GMP calculating results and the MPFR print-out.
The first image below is the case for the point of coordinate (22 0). (If you don't modify the program source downloaded, most probably you'll get the log with a start like it here. This is because I skipped the points ahead and started from column 22 when debugging. The code hasn't been cleaned up, so this is not removed.)
The meaning of the blue, green and red marking wireframes is the same as before. The ocherous wireframes marked the results calculated using GMP while printed out using MPFR. What's more, thickened wireframes in corresponding color are newly added. What they marked are absolutely accurate values and not high-precision approximate values. Orderly, the exact value of the real part, the approximate value of the real part, the exact value of the imaginary part, the approximate value of the imaginary part, the exact value of the square of z's modulus, the approximate value of the square of z's modulus calculated using my floating-point implementation are verified against GMP implementation.
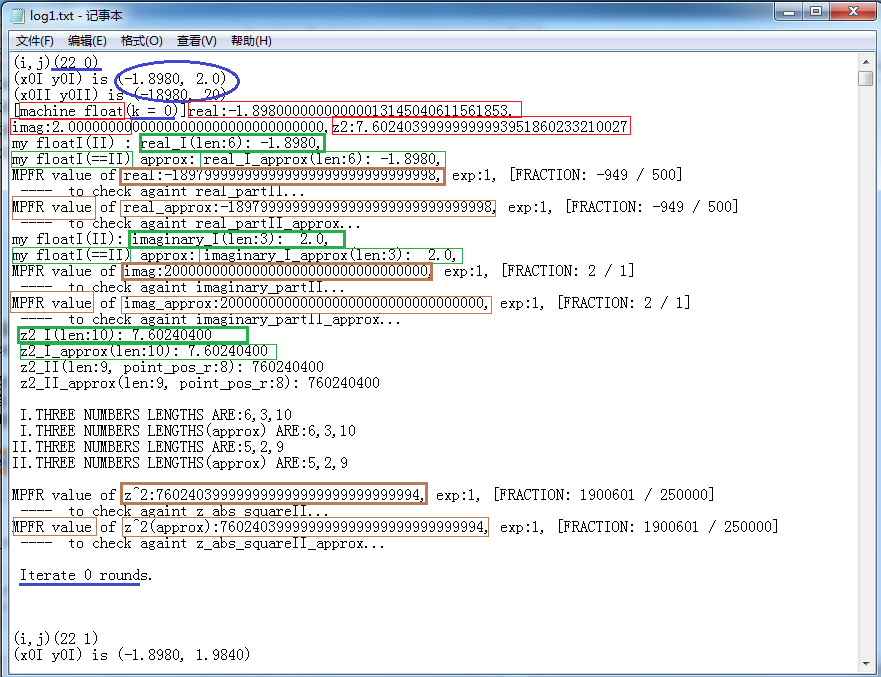
It finished wihile looping only once in the above illustration and got a short log. Let's further observe the k=9 time of iteration of
the point of coordinate (22 125). Now the log is very long and can't be all displayed in just one image. And here I can only
replace many middle lines of digits with one "*" line. In the first illustration below it accomplished the comparison between the exact
value of the real part and the approximate value of the real part:
In this second illustration below it accomplished the comparison between the exact value of the imaginary part and the
approximate value of the imaginary part. For this point is on the real axis with an imaginary part of 0, the log
is short.
Finally in this third illustration below it accomplished the comparison between the exact value of the square of z's modulus
and the approximate value of it.
The unmarked text part with words like "[FRACTION ... / ... ]" in these illustrations is the representation in fraction form that
GMP used, i.e., numerator / denominator, and it is irreducible.
This third program goes without GUI and got only pure calculation. The code now lies in main.cpp instead of View.cpp. All the newly added functions for GMP implementation begin with "GMP_" and lie in two files(mpfr_inc.h and mpfr_lib.c)(as above said, named after "mpfr"). I illustrate it below what to do to turn the pseudo-code before to GMP code:
(pseudo-code:)
x0(left );
y0(above);
a("2");
threshold("4.0");
for(i = 0; i < w; i++)
{
y0 = above;
for(j = 0; j < h; j++)
{
x("0");
y("0");
k = 0;
while(k++ < MAX_ITER)
{
real = x*x-y*y +x0;
imag = a*x*y +y0;
z_square = real*real + imag*imag;
if(z_square > threshold)
break;
else{
x = real;
y = imag;
}
}
y0 = y0 - delta;
}
x0 = x0 + delta;
}
x0(left );
y0(above);
a("2");
threshold("4.0");
for(i = 0; i < w; i++)
{
y0 = above;
for(j = 0; j < h; j++)
{
x("0");
y("0");
k = 0;
while(k++ < MAX_ITER)
{
real = x*x-y*y +x0;
imag = a*x*y +y0;
z_square = real*real + imag*imag;
if(z_square > threshold)
break;
else{
x = real;
y = imag;
}
}
y0 = y0 - delta;
}
x0 = x0 + delta;
}
(corresponding GMP implementaion)
GMP_init_calc()
GMP_reset_y0()
GMP_reset_x()
GMP_reset_y()
GMP_calc_real()
GMP_calc_imag()
GMP_calc_z_square()
if(GMP_cmp_threshold() > 0)
GMP_set_x_as_real()
GMP_set_y_as_imag()
GMP_update_y0()
GMP_update_x0()
GMP_clear()
GMP_init_calc()
GMP_reset_y0()
GMP_reset_x()
GMP_reset_y()
GMP_calc_real()
GMP_calc_imag()
GMP_calc_z_square()
if(GMP_cmp_threshold() > 0)
GMP_set_x_as_real()
GMP_set_y_as_imag()
GMP_update_y0()
GMP_update_x0()
GMP_clear()
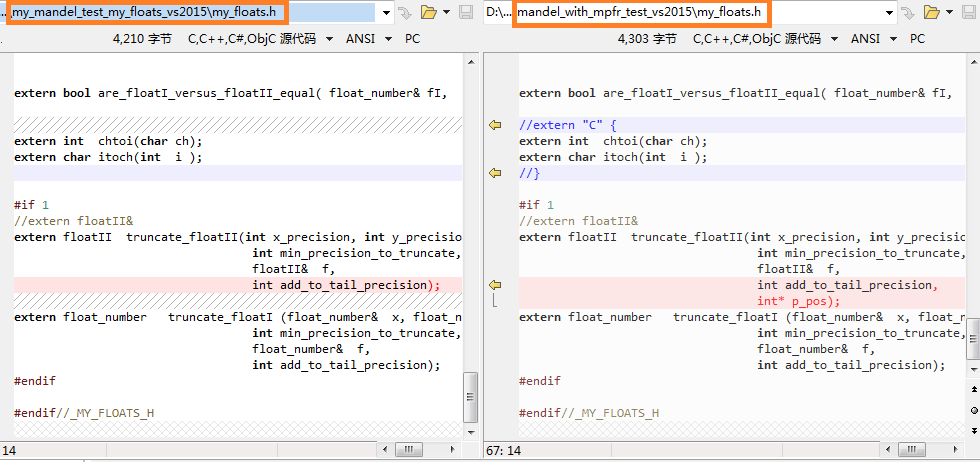
The only modification to my floating-point class code this third program made is: when an approximation is made to the (intermediate) calculated result of my floating-point implementation, to continue to compare the results and check the consistency of the two implementations, I need to make an corresponding approximation to the (intermediate) calculated result of GMP implementation. That is, I add one more parameter(p_pos) into the truncate_floatII() function to tell GMP implementation side: which decimal place I truncated at here, so that you must truncate correspondingly at that same decimal place of your value there.
Code before and after modification:
mandel_with_mpfr_test_vs2015\my_floats.h:
The corresponding modification to my_floats.cpp will be seen soon below.
extern floatII truncate_floatII(int x_precision, int y_precision, int delta_precision, int min_precision_to_truncate, floatII& f, int add_to_tail_precision, int* p_pos);
Currently truncate_floatI() is not modified. Because the results of floatI and floatII are the same, I only need to use one of them, currently I use floatII.
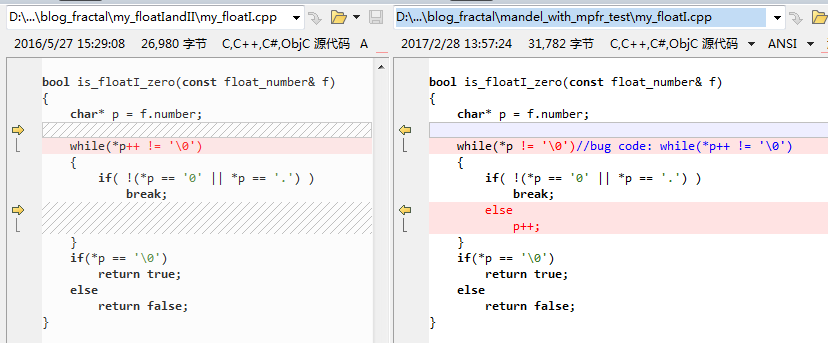
After GMP implementation was added, I found and corrected one (preliminary level, :-( ) bug in my_floatI.cpp(my_floatII.cpp is the same):
Why we need approximation yet? Because with absolutely accurate computation(not a bit approximation) the need for storage for the intermediate decimal result is incrementing exponentially by 2 to the power of the times of iteration. It counts in K for 10 times of iteration, and counts in M for 20 times of iteration. For 30 times of iteration it counts in G already. Besides, with computation like this on PC one becomes to feel a little slow already after about 10 times of iteration (i.e. a magnitude of 1000 digits times 1000 digits). So I have to do some approximation in the actual computation, for example, to let the need for storage increment linearly with the times of iteration. And take the speed of getting result into consideration.
Presently the algorithm for doing approximation I considered is roughly like this:
Step (0): Specify a requirement for the promotion of precision, e.g., 16 more decimal places of accuracy than the old ones;
Step (1): Specify the decimal places of accuracy, need to take these into consideration:
(A) the precision of starting coordinate,
(B) the precision of the step value between coordinates,
(C) incrementing with the times of iteration(?) ;
Step (2): Does the calculated result exceed the precision requirement? If not, do not modify the value of the result;
Step (3): If the answer is "yes" in step (2), count to the wanted decimal place of accuracy, then:
(A) if there is already significant digit in its front, then add at most e.g. 16 more decimal places after it.
(B) if there isn't any significant digit(i.e. all are '0's) in its front, unless being of value 0, find the first significant digit(non-zero one) after it, then add at most e.g. 16 more decimal places after that digit.
Its implementation:(taking floatII as the example) ((Highlighted lines of code is the modification of this function as said above.))
mandel_with_mpfr_test_vs2015\my_floatII.cpp:
floatII truncate_floatII(int x_precision, int y_precision, int delta_precision,
int min_precision_to_truncate,
floatII& f,
int add_to_tail_precision,
int* p_pos)
{
*p_pos = 0;
int truncate_part_len = 0;
int i;
//if(f.point_pos_r < min_precision_to_truncate)
// return f;
floatII approximation = f;
int max = x_precision ;
max = y_precision > max ? y_precision : max ;
max = delta_precision > max ? delta_precision : max ;
if(f.point_pos_r <= max)
return approximation;
max += add_to_tail_precision;
if(f.point_pos_r <= max)
return approximation;
else
truncate_part_len = f.point_pos_r - max;
max -= add_to_tail_precision;
//go to NO.`max' after '.' of f
/*
result (= x * y) ((precison of a by b )) :
(a) common case: (some non-'0' ahead)
0.02003004080509760000000001300xxxxxxxxxxxxxxxxx
(b) rare case: (all '0's ahead)
0.000000000000000000000000013000000050000xxxxxxxx
or 0.0000000000000000000000000130 (shorter vs. above)
*/
int len = strlen(f.digits);
int int_len = len - f.point_pos_r;
char* p = approximation.digits;
bool is_there_nonzero = false;
for(i = 0; i < (int_len + max); i++)
{
if(p[i] != '0')
{
is_there_nonzero = true;
break;
}
}
if(is_there_nonzero)
{
approximation.point_pos_r -= truncate_part_len;
int len2 = len - truncate_part_len;
memset(&p[len2], 0, truncate_part_len);
p[len2] = '\0'; //clear again ( redundant though)
*p_pos = len2 - int_len + 1;//*p_pos = &p[len2] - &p[int_len] + 1;
return approximation;// (.)
//531415
//0123456
// ^
}
else //TODO: to log and check this rare/corner case.
{
for(i = (int_len + max); i < len; i++)
{
if(p[i] != '0')
break;
}
if(i == len)
{
floatII result("0");
return result;
}
else
{
if( (len - i -1) <= add_to_tail_precision )
return approximation;
else
{
truncate_part_len = len - (i + 1 + add_to_tail_precision);
approximation.point_pos_r -= truncate_part_len;
memset(&p[i+1+add_to_tail_precision], 0, truncate_part_len);
*p_pos = i+1+add_to_tail_precision - int_len + 1;
return approximation;
}
}
}
}
The modification needed for the code that includes approximation:

The implementation of GMP truncating function in it: (taking GMP_truncate_real() as the example; the GMP_truncate_imag() code
just replace "real" with "imag".)
mandel_with_mpfr_test_vs2015\mpfr_lib.c:
The logic of this implementation of truncation is such: since all of the fractions in my program are designed to be
terminating decimals(not repeating decimals, needless to say irrational numbers), as to a calculated result which
has the form like "53.1415926" etc., let it times 10 to the power of an incrementing integer variable(which will be
equal to its decimal places) until the product becomes an integer (the rule for judgement is the denominator becomes 1),
then go to the position to truncate as specified, set the digit itself and those after it to '0', use this new string
to construct a new mpq_t type number, then divide this new number by 10 to the power of the corresponding number.
Thus we accomplished the truncation of the calculated result.
void GMP_truncate_real(char* str_numerator, char* str_denominator,
char* str_gmp_mpfr, int* p_exp, int mpfr_precision,
int len, int trunc_pos)
{
mpz_t numerator;
mpz_t denominator;
mpq_t a;
mpfr_t f1, f2;
mpfr_exp_t exp;
mpz_init(numerator);
mpz_init(denominator);
mpq_init(a);
mpq_set(gmp_real_approx, gmp_real);
if(trunc_pos == 0)
{
//return;
}
else
{
int n;
char* str;
char* p;
mpz_set(denominator, mpq_denref(gmp_real_approx));
//gmp_printf("denominator is %Zd\n", denominator);
mpq_set_si(a, 10, 1);
n = 0;
while( mpz_cmp_si(denominator, 1) != 0)
{
mpq_mul(gmp_real_approx, gmp_real_approx, a);
//gmp_printf("%#040Qd\n", gmp_real_approx);
mpz_set(denominator, mpq_denref(gmp_real_approx));
n++;
}
//printf("\n multiplied by 10^ %d\n" , n);
mpz_set(numerator, mpq_numref(gmp_real_approx));
//gmp_printf("numerator is %Zd\n", numerator);
str = (char*)malloc(len+16); //some more space
memset(str, 0, len+16);//buggy: memset(str, 0, sizeof(str));
mpz_get_str(str, 10, numerator);
//printf("str got:%s\n", str);
p = str + strlen(str);
p -= (n-trunc_pos)+1; //53.1415926
while( *p != '\0')
*p++ = '0';
mpq_set_str(gmp_real_approx, str, 10);
mpq_canonicalize(gmp_real_approx);
while(n > 0)
{
mpq_div(gmp_real_approx, gmp_real_approx, a);
//gmp_printf("%#040Qd\n", approx);
n--;
}
free(str);
}
mpz_set(numerator, mpq_numref(gmp_real_approx));
mpz_get_str(str_numerator, 10, numerator);
mpz_set(denominator, mpq_denref(gmp_real_approx));
mpz_get_str(str_denominator, 10, denominator);
//for visualizing the string
mpfr_init2(f1, (mpfr_prec_t)mpfr_precision);
mpfr_init2(f2, (mpfr_prec_t)mpfr_precision);
mpfr_set_z(f1, numerator , MPFR_RNDZ);
mpfr_set_z(f2, denominator, MPFR_RNDZ);
mpfr_div(f1, f1, f2, MPFR_RNDZ);
mpfr_get_str(str_gmp_mpfr, &exp, 10, 0, f1, MPFR_RNDZ);
*p_exp =(int)exp;
mpfr_clear(f1);
mpfr_clear(f2);
mpz_clear(numerator);
mpz_clear(denominator);
mpq_clear(a);
}
In the function code, the highlighted line 30 obtained the denominator, line 32 is the multiplier 10 to be used, we can see the loop of multiplying by 10 and checking if the denominator becomes 1 at line 34 and line 36. Line 43 obtained the current numerator, the highlighted line 48 obtained the current string of the numerator. Line 50 to 53 set the part to be truncated of this string to all '0'. After constructing the new GMP fraction at line 55, we can see the highlighted line 57 and line 59 loop to divide the new number by 10 to the power n.
So far, we haven't looked at the addition and multiplication code yet. Though it's only primary school arithmetic, below we'll take a rough look at it. Although on the above the GMP shows it is really powerful so maybe to use GMP(and MPFR) to do more computation will be a better choice later (because it allows people to use fractions, that is, repeating decimals, and other functions etc. that I myself haven't got ), it might be better to have one more kind of implementation in parallel when available. However, if not available, I can just use GMP.
Here I take the floatII class as the example, the implementation code of floatI class is longer, the floatII code is more concise, both of their algorithms are the same. There isn't very much to say about addition:
mandel_with_mpfr_test_vs2015\my_floatII.cpp:
It prepares to align the decimal point beginning from the highlighted line 7. Line 20 obtained the position of the decimal point.
Line 24 and 25 supplement '0's in an aligning style. Line 27 is about to do addition if the signs of the two numbers are the same.
Its next line of code begins to do the addition, recording the carry value. Beginning from line 57 it prepares for the result string,
which reads from left to right, while the addition itself is done from the lower to the higher, i.e., from right to left.
Line 66 constructs the object of fII class using the string and returns from the function.
Line 84 is about to do subtraction for the signs of the two numbers are different. First it does comparison between their absolute
values to decide which one is larger and what the sign of the difference will be. Line 94 shows that they are equal so the code
returns 0. Line 104 is about to subtract the smaller absolute value from the larger one. Next it does subtraction, borrowing,etc.
When done it likewise constructs the string, then constructs the object of fII class. Thus done.
floatII floatII::operator+ ( floatII& f2)
{
//TODO: 0?
int sign, pos;
//align point
floatII f1 = *this;
int int_len1 = strlen(f1.digits) - f1.point_pos_r;
int int_len2 = strlen(f2.digits) - f2.point_pos_r;
int frac_len1 = f1.point_pos_r;
int frac_len2 = f2.point_pos_r;
int max_int_len = int_len1 >= int_len2 ? int_len1 : int_len2 ;
int max_frac_len = frac_len1 >= frac_len2 ? frac_len1 : frac_len2;
floatII f1_old = f1;
floatII f2_old = f2;
//pos
pos = max_frac_len;
int len = max_int_len + max_frac_len;
char* s1 = f1.extend_zero2( max_int_len-int_len1, max_frac_len-frac_len1);
char* s2 = f2.extend_zero2( max_int_len-int_len2, max_frac_len-frac_len2);
if(f1.minus == f2.minus)
{
//minus assign
sign = f1.minus? -1 : +1;
int* carry = (int* )malloc( (len+1) *sizeof(int));
char* r = (char* )malloc( len );
memset(carry, 0, (len+1)*sizeof(int));
char* q = s1+len-1;
char* p = s2+len-1;
int m;
int k = 0;
while(q >= s1)
{
m = chtoi(*q) + chtoi(*p) + carry[k];
if(m >= 10)
{
carry[k+1] += 1;
r[k] = itoch(m-10);
}
else
{
r[k] = itoch(m);
}
p--;
q--;
k++;
}
char* str = (char* )malloc(len+1+1); //doesn't care if more
int i = 0;
int j;
if(carry[k] > 0)
str[i++] = itoch(carry[k]);
for(j = 0; j < len; j++)
str[i++] = r[len-1-j];
str[i] = '\0';
floatII str_result(str, sign, pos);
free(str); //? do it in destructor?
free(r);
free(carry);
free(s1);
free(s2);
return str_result;
}
else
{
//to decide sign
char* p = s1;
char* q = s2;
while(*p != '\0') // && *q != '\0'
{
if(chtoi(*p) != chtoi(*q))
break;
p++;
q++;
}
if(*p == '\0')
{
free(s1);
free(s2);
floatII f4("0");
if(MY_DEBUG) printf("they are equal,minus result is 0\n");
return f4;
}
else
{
bool t = chtoi(*p) > chtoi(*q) ? f1.minus : f2.minus;
sign = t? -1 : +1;
char* big = (*p > *q) ? s1 : s2;
char* small = (*p > *q) ? s2 : s1;
p = big + len-1;
q = small + len-1;
int* borrow = (int* )malloc( (len) *sizeof(int));
int n;
char* r = (char* )malloc( (len));
memset(borrow, 0, (len)*sizeof(int));
int k = 0;
while(p >= big)
{
if( (chtoi(*p) + borrow[k]) >= chtoi(*q))
{
n = chtoi(*p) + borrow[k] -chtoi(*q) ;
}
else
{
char* l = p-1;
while( chtoi(*l) == 0 )
{
*l = '9';
l--;
}
borrow[k] = 10;
*l -= 1;
n = chtoi(*p) + borrow[k] - chtoi(*q) ;
}
r[k] = itoch(n);
p--;
q--;
k++;
}
//TODO: to remove leading 0s in integer part
char* str = (char* )malloc(len+1);
int i = 0;
int j;
for(j = 0; j < len; j++)
str[i++] = r[len-1-j];
str[i] = '\0';
floatII str_result2(str, sign, pos);
free(str);
free(r);
free(borrow);
free(s1);
free(s2);
return str_result2;
}
}
}
The multiplication costs two "*" operator overloading functions, however. The multiplication of two objects of the class is transformed to first doing multiplications of one object of the class and one integer variable(i.e., a number multiplied by every digit of another number), then summing them up after shifting their decimal points correspondingly. (For example, if we got to calculate $f_{1}$ * $f_{2}$, in which $f_{2}$ is of the form "xyzwr.st0", then the result would be $$ \begin{aligned} result & = f_{1} * x * 10^m \space \space \space \space \space \space \text{(m=max_int_len-1)} \\ & + f_{1} * y * 10^{m-1} \\ & + f_{1} * z * 10^{m-2} \\ & + ... \\ & + f_{1} * t * 10^{-2} \\ & + f_{1} * 0 * 10^{-3} \space \space \space \space \space \space \text{(-3=-max_frac_len)} \end{aligned} $$ ). Thus I used two operator overloading functions.
mandel_with_mpfr_test_vs2015\my_floatII.cpp:
The highlighted lines are those illustrated above. In the first function it does carrying similar to that in addition.
floatII floatII::operator* (int m) // 0<=m<=9
{
//TODO: 0?
int sign, pos;
floatII& f1 = *this;
sign = f1.minus? -1: +1; //does not care
//pos
pos = f1.point_pos_r; //doesn't change
int len = strlen(f1.digits);
char* s = f1.digits;
int* carry = (int* )malloc( (len+1) *sizeof(int));
char* r = (char* )malloc( (len));
memset(carry, 0, (len+1)*sizeof(int));
char* q = s+len-1;
int d;
int k = 0;
while(q >= s)
{
d = chtoi(*q) * m + carry[k];
if(d >= 10)
{
carry[k+1] += d/10;
d = d % 10;
}
r[k] = itoch(d);
q--;
k++;
}
//copied from add operation code part
char* str = (char* )malloc(len+1+1); //doesn't care if more
int i = 0;
int j;
if(carry[k] > 0)
str[i++] = itoch(carry[k]);
for(j = 0; j < len; j++)
str[i++] = r[len-1-j];
str[i] = '\0';
floatII str_result(str, sign, pos);
free(str); //? do it in destructor?
//copied from add operation code part -- end
free(r);
free(carry);
return str_result;
}
floatII floatII::operator* (const floatII& f2)
{
//TODO: 0?
int sign; // pos;
floatII& f1 = *this;
if(f1.minus == f2.minus)
sign = +1;
else
sign = -1;
char*p = f1.digits;
char*q = f2.digits; //(choose the shorter to be multiplier?)
floatII multi("0");
int len2 = strlen(f2.digits);
for(int i = 0; i < len2; i++)
{
floatII t1 = f1 * chtoi(q[i]);
floatII t2 = shift_floatII(t1, len2 - f2.point_pos_r - 1 - i);
multi = multi + t2;
}
multi.minus = (sign==-1)? true : false;
return multi;
}
floatII& shift_floatII (floatII& f, int m)
{
if(m > 0)
{
if(m >= f.point_pos_r)
{
f.extend_zero(0, m - f.point_pos_r);
f.point_pos_r = 0;
}
else
f.point_pos_r -= m;
}
else if(m < 0)
{
int int_len = strlen(f.digits) - f.point_pos_r;
if(-m >= int_len)
f.extend_zero(-m-int_len+1, 0);
f.point_pos_r += -m;
}
return f;
}
Having long been a c programmer up until now, I know very little about c++. It looks more natural using operator overloading in c++ to operate on the floating-point number class. However, it feels more portable for c libraries than c++ libraries when one is using GMP.
Once I found the memory usage of the third program soon went too high, and it kept increasing. After debugging I found it out that some pieces of code modifying "malloc/free" as "new/delete" led to this problem. This is not memory leak yet, for the memory is restored as soon as one closes the program. But under such memory usage the program will soon be not able to run. It seems the memory allocated through "new" has not been returned to the OS quickly after "delete", while "free" does. Since the program does large amount of computation persistently, no memory leak is crucial to the program.
It is rather good that the result of my implementation is consistent with GMP computation, using not very much code. GMP uses the fraction form, this enlarges the range of operation greatly compared to using decimal form by me. Surely it got a more complicated algorithm. The algorithm of mine is only for multiplication and addition, so it is just suitable for computing Mandelbrot set(I don't know if it is well suitable for computing Julia set.) and may not be enough for computation of other fractals.
Besides Win/VC, I would like to implement it on Linux/GTK.
I ever thought it was best to distribute the programs on ReactOS. But I tried ReactOS on VMWare and found its compatiblitly and stability were not suitable for actual use yet. ......
(P.S.: The precision in MPFR means binary precision, this may not easily match the decimal precision I adopted in my floating-point implementation.)
I try to build a Mandelbrot set image gallery, here attached is the PHP frontend and c backend. Refer to the PDF e-book and shell etc. for making it. But because of the high performance needed for computing, more precise computation is not practical yet.