采用复旦大学姚慕生第一版的教科书:p(182-)184页 例6
$$
\begin{aligned}
(N_1) \leftarrow \rightarrow Q(\sqrt{2})
\end{aligned}
$$
$$
\begin{aligned}
(N_2) \leftarrow \rightarrow Q(i)
\end{aligned}
$$
$$
\begin{aligned}
(N_3) \leftarrow \rightarrow Q(i\sqrt{2})
\end{aligned}
$$
$$
\begin{aligned}
(N_4) \leftarrow \rightarrow Q(\sqrt{2}, i)
\end{aligned}
$$
$$
\begin{aligned}
(H_1) \leftarrow \rightarrow Q(i\sqrt[4]{2})
\end{aligned}
$$
$$
\begin{aligned}
(H_2) \leftarrow \rightarrow Q(\sqrt[4]{2} )
\end{aligned}
$$
$$
\begin{aligned}
(H_3) \leftarrow \rightarrow Q(\sqrt[4]{2} (1+i))
\end{aligned}
$$
$$
\begin{aligned}
(H_4) \leftarrow \rightarrow Q(\sqrt[4]{2} (1-i))
\end{aligned}
$$
上边箭头右边这些个中间域是怎么得出来的?
背景:八个子群(p184): $$ \begin{aligned} (N_1) & = \left\{ 1,\xi, \eta^2 , \xi\eta^2 \right\} \\ (N_2) & = \left\{ 1, \eta , \eta^2 , \eta^3 \right\} \\ (N_3) & = \left\{ 1, \eta^2 , \xi\eta, \xi\eta^3 \right\} \\ (N_4) & = \left\{ 1, \eta^2 \right\} \\ (H_1) & = \left\{ 1,\xi \right\} \\ (H_2) & = \left\{ 1,\xi\eta^2 \right\} \\ (H_3) & = \left\{ 1,\xi\eta \right\} \\ (H_4) & = \left\{ 1,\xi\eta^3 \right\} \end{aligned} $$ $$ \begin{aligned} \xi : \sqrt[4]{2} \rightarrow -\sqrt[4]{2} \\ i\sqrt[4]{2} \rightarrow i\sqrt[4]{2} \\ -\sqrt[4]{2} \rightarrow \sqrt[4]{2} \\ -i\sqrt[4]{2} \rightarrow -i\sqrt[4]{2} \end{aligned} $$ $$ \begin{aligned} \eta : \sqrt[4]{2} \rightarrow i\sqrt[4]{2} \\ i\sqrt[4]{2} \rightarrow -\sqrt[4]{2} \\ -\sqrt[4]{2} \rightarrow -i\sqrt[4]{2} \\ -i\sqrt[4]{2} \rightarrow \sqrt[4]{2} \end{aligned} $$ 对$N_1$课本上有说明。
$N_2$保持$i$不变容易看出。
对$H_1$和$H_2$,下图中容易看出$\alpha_1$和$\alpha_2$分别对其不变:

对$H_3$的理解,看下图;
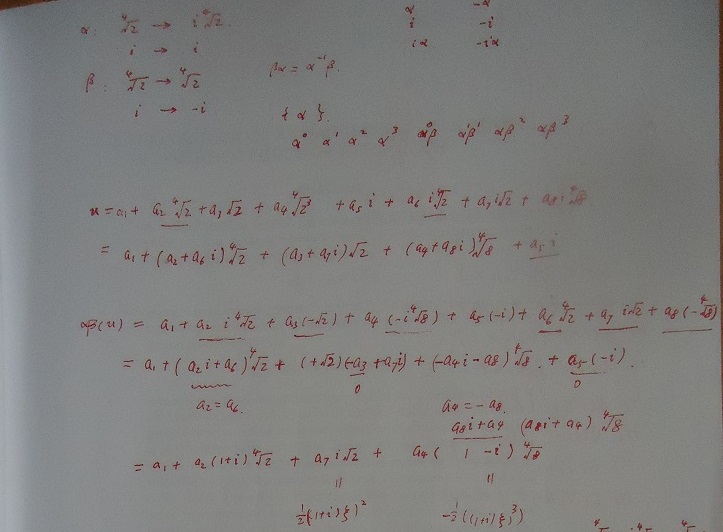
对$N_4$,下图中可看到基底是$\sqrt{2}$和$i$:

$H_4$的理解与$H_3$相仿,看下图:

对$N_3$,可以验证$i\sqrt{2}$对${\xi\eta}$不变如上图;且其对${\eta^2}$不变,由此对${\xi \eta^3}$即${\xi\eta \eta^2}$不变。
开始我不清楚它($Q(i\sqrt{2})$中的$i\sqrt{2}$)是怎么得出来的?现在有了下图清楚了:

附上资料(专业人士的阐述): Computation for the Galois group of a polynomial.pdf
以及:
physicsforums
参考文献:
Spindler: Abstract Algebra with Applications, vol.2 p409
Fraleigh: A First Course in Abstract Algebra p460
Menini & Oystaeyen: Abstra Algebra: A Comprehensive Treatment p592
Beachy & Blair : Abstract Algebra p402
《从一元一次方程到伽罗瓦理论》p104
《伽罗华理论基础》 p99
其他还有:
List Gaal: Classical Galois Theory with Examples p99
John Howie: Fields and Galois Theory p124
《代数学引论》p253
《近世代数概论》下册 p550
《近世代数基础》刘绍学 p150