量子物理中,玻尔的量子论的基本原理之一就是说:原子在基态等定态不辐射。电动力学的教科书也说:“原子处于基态时是稳定的,不会产生
辐射,这点是和经典理论(经典电动力学)有深刻矛盾的”。原因是按卢瑟福原子模型,电子在其中作加速近圆周运动,会不断辐射电磁波,在
极短时间内就要损失全部能量,使这一模型不稳定而崩溃。算了一下,假设氢原子电子在n=1的玻尔半径上圆周运动,圆频率为$10^{16}$数量级 $^{\dagger\dagger}$ ,
如果电子象经典电动力学说的辐射,且以这个频率辐射电磁波,这个频率是高频,在可见光高频范围之上,对应波长为数百Å
(原子线度是1Å,可见光波长约为数千Å)。《新概念物理 量子物理》中说道:“如果没有能量补充,电子的轨道将
不断缩小,最后被吸引到原子核上面去”。
浏览了一些《伯克利物理学教程第三卷 波动学》、MIT《振动与波》的内容,了解到不独量子力学,机械振动也有本征态的概念,比如驻波态。
于是就问:(从)非驻波态能不能变成驻波态;驻波本征态之间的变化;如何从非驻波态形成驻波态(比如反射);一个驻波本征态如何
变为非(该)本征态并变为另一个驻波本征态。
一般的说法,驻波没有能量的传播。应该说是驻波不吸收/释放净能量。《新概念物理 力学》中说道“怎样……形成驻波?通常靠反射。”
振动波的能量传播透不过势垒,波被势垒完全反射回来,于是叠加形成驻波。所以开始我想(比如H原子的例子)电子辐射的电磁波是否也有遇到什么
被势垒反射/散射的机制,然后被电子又吸收,从而我们处在势垒外面观察的结果,完全没有任何能量透射出来(于是以为玻尔的说法:基态的氢原子
不辐射)。
但是这种想法似乎离(我所知的)事实比较远。考察电子所处的环境,电子向外辐射电磁波,没听说有什么会将电子辐射的电磁波反射回去的。
即便有,电子又怎么能恰巧将其完全吸收?这种图象比较奇异(或许电磁阻尼可以考虑)。但考察电子所处的环境,我想到:现实中,带电粒子
(如电子)总是处于热辐射场中,因此要振动、吸收和辐射。于是我思索怎么了解电子从电磁场中吸收了多少(比如象考虑在黑体辐射腔内放H原子的
图象),这也是一些热辐射与热平衡方面的问题。翻了翻一些微波的书,似乎没找到。一天,读到吴大猷书中介绍的瑞利-金斯公式的推导,我觉得
找到了正好解决了我的问题的答案。
这个推导表明:电子从电磁场中吸收的能量能够恰好等于它辐射的能量。从而现在认为:原子电子在基态不一定不辐射,只是辐射与吸收平衡。
${\overline p = {1 \over {4 \pi \epsilon_{0}}} { {e^2 a^2 \omega^4} \over {3 c^3} }}$
(电动力学教科书)
(电动力学教科书)
( $\psi = {1 \over {4 \pi \epsilon_{0}}} w $ ?)
((Sturm-Liouville问题也有名为Parseval等式的公式,见《古今数学思想》))
积分区域扩大为矩形
$\psi_{\nu} d \nu = {8 \pi kT \over c^3 } \nu^2 d \nu $
读到吴大猷在他的著作《理论物理-量子论与原子结构》p18(附录2 Rayleigh-Jeans定律)中写道:
“
Rayleigh-Jeans定律亦可纯由电动力学得之。
一个一维单谐振子的辐射率为: $$ \begin{aligned} p & = { \omega_{0}^4 (ea)^2 \over 3c^3 } \\ & = { 2 \omega_{0}^2 e^2 \over 3mc^3 } \epsilon, \space \space \space \space \space \space \epsilon = {1 \over 2} m(a \omega_{0})^2 \end{aligned} \tag{I-32/I-32a} $$ $\epsilon$ 为振子之能量。
兹计算一个单谐振子在电磁场吸收能量的率。设振子频率为$\omega_{0}$,同(10)式,其在电场E之运动方程式为 $$ \begin{aligned} \ddot{x} + \omega_{0}^2 x = {e \over m} E_{x} \end{aligned} \tag{I-33} $$
设在$ 0 \leqslant t \leqslant T $间,$\vec{E}$ 之x分量$E_{x}$可作Fourier变换如下 $$ \begin{aligned} E_{x}(t) & = {1 \over 2\pi} \int_{- \infty}^{\infty} f(\omega) e^{i \omega t} d \omega \\ f(\omega) & = \int_{0}^{T} E_{x}(t) e^{-i \omega t} dt \\ E_{x}(t) & = 0 \space \space \space \space \space \space {t \lt 0} \space \space \space {t \gt T} \end{aligned} \tag{I-34} $$
$E_{x}(t)$为一实数之条件为 $$ \begin{aligned} f^{*}(\omega) = f(- \omega) \end{aligned} \tag{I-35} $$
$E_{y}(t)$、$E_{z}(t)$分量亦同此。按电动力学,此电磁场之辐射能密度$\psi$为下列平均值(对时间作平均) $$ \begin{aligned} \psi & = {1 \over {8 \pi} } {\overline {(E^2 + H^2)}} = {1 \over {4 \pi} } {\overline {E^2}} \\ & = {3 \over {4 \pi} } {\overline {E_{x}^2}} \end{aligned} \tag{I-36} $$
由(34)式,即得: $$ \begin{aligned} {\overline {E_{x}^2}} & = {1 \over T} \int_{0}^{T} {E_{x}}^2 dt \\ & = {1 \over {2 \pi T}} \int_{0}^{T} E_{x} dt \int_{- \infty}^{\infty} f(\omega) e^{i \omega t} d {\omega} \\ & = {1 \over {2 \pi T}} \int_{- \infty}^{\infty} f(\omega) d {\omega} \int_{0}^{T} E_{x} e^{i \omega t} dt \\ & = {1 \over {2 \pi T}} \int_{- \infty}^{\infty} f(\omega) f^{*}(\omega) d {\omega} \\ & = {1 \over {\pi T}} \int_{0}^{\infty} {|f(\omega)|}^2 d \omega \end{aligned} $$
故能量密度在$\omega$与$\omega + d \omega$间者为$(\omega = 2 \pi \nu)$ $$ \begin{aligned} \psi_{\omega} & = {3 \over {4 \pi^2 T}} {|f(\omega)|}^2 \\ 或 \psi_{\nu} & = {3 \over {2 \pi T}} {|f(\nu)|}^2 \end{aligned} \tag{I-37} $$
(33)方程式之解为 $$ \begin{aligned} x(t) & = {e \over {\omega_{0} m}} \int_{0}^{t} E_{x}(\xi) \sin{ \omega_{0} } (t - \xi) d \xi \\ x(0) & = \dot{x} (0) = 0 \end{aligned} \tag{I-38} $$
$E_{x}$对振子每秒钟所作之功为 $$ \begin{aligned} \Delta{\omega} & = {e \over T} \int_{0}^{T} \dot{x} E_{x} dt \\ & = {e^2 \over {mT} } \int_{0}^{T} E_{x}(t) dt \int_{0}^{t} E_{x}(\xi) \cos{ \omega_{0} } (t - \xi) d \xi \\ & = {e^2 \over {mT} } \int_{0}^{T} E_{x}(\xi) d \xi \int_{\xi}^{T} E_{x}(t) \cos{ \omega_{0} } (t - \xi) dt \space \space \space \space \space \space \space \space \dagger \\ & = {e^2 \over {2mT} } \int_{0}^{T} E_{x}(t) dt { \left \{ \int_{0}^{t} + \int_{t}^{T} \right \} } E_{x}(\xi) \cos{ \omega_{0} } (t - \xi) d \xi \\ & = {e^2 \over {4mT} } { \left \{ {\int_{0}^{T} E_{x}(t) e^{i \omega_{0} t} dt \int_{0}^{T} E_{x}(\xi) e^{-i \omega_{0} \xi} d \xi + \int_{0}^{T} E_{x}(t) e^{-i \omega_{0} t} dt \int_{0}^{T} E_{x}(\xi) e^{i \omega_{0} \xi} d \xi } \right \} } \\ & = {e^2 \over {2mT} } {|f(\omega)|}^2 \space \space \space \space \space \space \space \space \text{由(34)} \\ & = {{\pi e^2} \over {3m}} \psi_{\nu} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \text{由(37)} \end{aligned} \tag{I-39} $$
在稳定状态下,单谐振子的辐射率(32)必与其吸收能率(39)相等,亦即 $$ \begin{aligned} \psi_{\nu} = { {8 \pi \nu^2} \over c^3 } \epsilon \end{aligned} $$
如以古典物理之“能之等分配律”$\epsilon = kT $值用于此式,即得Rayleigh-Jeans定律。
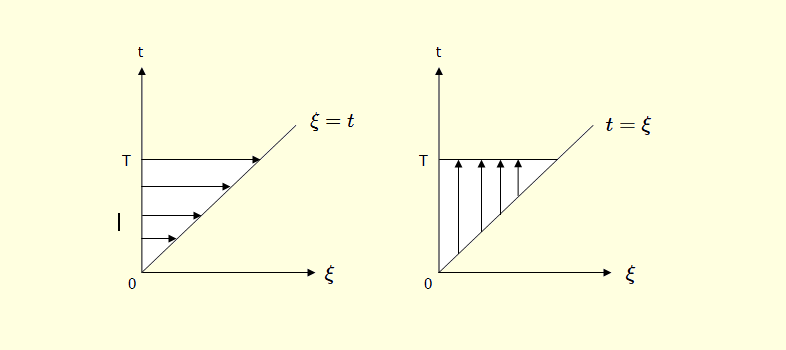
$\dagger$ 注: $ \int_{0}^{T} E(t)dt \int_{0}^{t} E(\xi) \cos \omega (t - \xi) d \xi $ 积分乃左图横线之面积,
$ \int_{0}^{T} E(\xi)d \xi \int_{\xi}^{T} E(t) \cos \omega (t - \xi) dt $ 积分则系右图竖线之面积。故上二式相等。
”
[参考]
《理论物理-量子论与原子结构》吴大猷
Men of Physics: Lord Rayleigh - The Man and his Work by Robert Bruce Lindsay
https://en.wikipedia.org/wiki/John_William_Strutt,_3rd_Baron_Rayleigh
https://en.wikipedia.org/wiki/Rayleigh-Jeans_law
Advanced Concepts in Quantum Mechanics (Appendix 2.A) by Giampiero Esposito (p46)
据说Rayleigh在1900年根据能量均分定理导出了今天所知的Rayleigh-Jeans定律;在1905年Rayleigh和Jeans又给出了更完整的推导和微小修正。
我没找到原论文(谁能提供将非常感谢)。不知其论文是否用这里吴大猷所说的纯电动力学的方法。
未找到这里所说的(10)式。
(密度对全空间体积平均?)
( $ E_{x}$, $ E_{y}$, $ E_{z}$ ?)
( $ E_{x}$, $ E_{y}$, $ E_{z}$ ?)
傅里叶变换有parseval等式
$$ \begin{aligned} \int_{-\infty}^{\infty} {|f(\omega)|}^2 d \omega \end{aligned} $$ $$ \begin{aligned} = 2 \pi \int_{-\infty}^{\infty} {|g(x)|}^2 dx \end{aligned} $$
$$ \begin{aligned} \int_{-\infty}^{\infty} {|f(\omega)|}^2 d \omega \end{aligned} $$ $$ \begin{aligned} = 2 \pi \int_{-\infty}^{\infty} {|g(x)|}^2 dx \end{aligned} $$
$$
\begin{aligned}
\psi & = {3 \over 4 \pi^2 T }\int_{0}^{\infty} {|f(\omega)|}^2 d \omega \space \space \space \text{;} \\
& = \int_{0}^{\infty} \psi_{\omega} d \omega \\
& = \int_{0}^{\infty} \psi_{\nu} d \nu
\end{aligned}
$$
得出这个方程式的这个解很厉害。我不知道这个方程是怎样解的;只会验证这个解,用数学分析中含参变量的积分的求导公式:
$$
\begin{aligned}
{d \over dx } \int_{\alpha (x)}^{\beta (x)} f(x,y)dy
\end{aligned}
$$
$$
\begin{aligned}
& = \int_{\alpha (x)}^{\beta (x)} { {\partial f(x,y)} \over {\partial x}} dy \\
& + f[x, \beta (x)] \beta^{\prime}(x) \\
& - f[x, \alpha (x)] \alpha^{\prime}(x)
\end{aligned}
$$
傅里叶变换实数形式:
$$
\begin{aligned}
f(t) = {1 \over \pi } \cdot
\end{aligned}
$$
$$
\begin{aligned}
\int_{0}^{\infty} d \omega \int_{- \infty}^{\infty} f(\tau) \cos \omega (t- \tau) d \tau
\end{aligned}
$$
我使用的版本原文将后一式中的
$$
\begin{aligned}
E(t) \cos \omega (t - \xi) dt
\end{aligned}
$$
误为
$$
\begin{aligned}
E(t) \cos \omega (t - \xi) d \xi
\end{aligned}
$$
对以上的内容自己作了一些计算来理解。
(1) 关于谐振子的辐射率
按照电动力学教科书里的公式,加速电荷的辐射功率 $$ \begin{aligned} P = {1 \over {4 \pi \epsilon_{0}}} {2 \over 3} { {e^2 {\dot{\vec v}}^2} \over c^3 } \end{aligned} $$ 简谐振子的能量记为 $ W = {1 \over 2} m {\dot{z}}^2 + {1 \over 2} k z^2 = {1 \over 2} m a^2 {\omega}^2 $ ,设 $z = a \cos {\omega t} $ , 则 $\vec v = \dot z = -a \omega \sin {\omega t} $, $ \dot{\vec v} = \ddot z = -a {\omega}^2 \cos {\omega t} $ , 故 $ P = {1 \over {4 \pi \epsilon_{0}}} {2 \over 3} { e^2 a^2 {\omega}^4 {\cos}^2 {\omega t} \over c^3 } $ 。
计算平均值$ {1 \over T} \int_{0}^{T} {\cos}^2 {\omega t} dt $ ,使用 $ T = {1 \over \nu} = { {2 \pi} \over \omega } $ ,为$ 1 \over 2 $ , 所以有${\overline p = {1 \over {4 \pi \epsilon_{0}}} { {e^2 a^2 \omega^4} \over {3 c^3} }}$。比例因子为不同单位制之间的差异,故有原文 辐射率的式子。
(2) 关于(33)方程式之解的验算
如旁注,直接套公式即得: $$ \begin{aligned} \dot x & = {e \over {\omega_{0} m}} \int_{0}^{t} \omega_{0} E_{x}(\xi) \cos {\omega_{0} (t - \xi) d \xi} + E_{x}(t) \sin \omega_{0}(t-t) \\ \ddot x & = { {e \omega_{0}} \over {\omega_{0} m} } \left [ \int_{0}^{t} \omega_{0} E_{x}(\xi) (- \sin {\omega_{0} (t - \xi)) d \xi} + E_{x}(t) \cos \omega_{0}(t-t) \right ] \end{aligned} $$ 代入左端计算即得。
(3) (I-39)中一步的验算
将积分式 $$ \begin{aligned} \int_{0}^{T} E_{x}(\xi) d \xi \int_{\xi}^{T} E_{x}(t) \cos{ \omega_{0} } (t - \xi) dt \end{aligned} $$ 中的变量符号改变一下,不影响积分值,对换$ t $ 与 $ \xi $ $$ \begin{aligned} \int_{0}^{T} E_{x}(t) dt \int_{t}^{T} E_{x}(\xi) \cos{ \omega_{0} } (\xi - t) d \xi \end{aligned} $$ 所以有中间那一步。
(4) 关于(I-37)式
还未很好地理解。疑为$ \psi_{\nu} = {3 \over {2 \pi T}} {|f(\omega)|}^2 = {3 \over {2 \pi T}} {|f(2 \pi \nu)|}^2 $ , 后面(I-39)式的最后好象也支持这一点。
为什么我觉得找到答案了呢?该推导从辐射率与吸收率平衡出发,导出了Rayleigh-Jeans公式。好了,现在Rayleigh-Jeans定律成立(至少在
一定范围内(长波部分,低频?)成立),按照它来计算的话,自然将得到吸收率恰好等于辐射率;这正是我需要的。
推而广之,电子在任何本征态都不一定不辐射,只是辐射与吸收动态平衡。
(而在激发态寿命很短的情况下,这一平衡是极其短暂的。激发本征态为什么很快向基态本征态迁移?机械振动似乎不是这样(?)。
激发本征态为什么不是(热)平衡态?)。
如果我有条件做实验,先着手这个方向去做。
$\dagger\dagger$ (套用一些公式: $ m_{e} {v^2 \over r} = k {e^2 \over r^2} $, 取r为玻尔半径,$ r = a_{0} = {4 \pi \epsilon_{0}} {{\hbar}^2 \over {m_{e} e^2} } $ , 于是可得 $ v_{0}^2 = { {k^2 e^4} \over {\hbar}^2 } $ , 动能 $ T = { {1 \over 2} m_{e} v^2 } = { {1 \over 2} { m_{e} {k^2 e^4} \over {\hbar}^2 } } $ , 势能$ U = -k {e^2 \over r} = -k^2 {m_{e} \over {\hbar}^2} e^4 $ ;
可见 $ T = -{1 \over 2} U $ 。 电子基态能量$ -13.6eV=T+U=-T={1 \over 2} U $ 。用 $ { {1 \over 2} m_{e} v_{0}^2 } = 13.6eV $ 得: $ v_{0}^2 = {2 \times 13.6} \cdot {e \over m_{e}} = {2 \times 13.6} \cdot { {1.6 \times 10^{-19}} \over {9.1 \times 10^{-31}}} $ , 解得$ v_{0} \approx {2.18 \times 10^6}(m/s) $ 。
或者用 $ v_{0}^2 = { {k^2 e^4} \over {\hbar}^2 } $ , 从而 $ v_{0} = k \cdot {{e^2 \cdot {2 \pi}} \over h} = 9 \times 10^9 \cdot { {2.56 \times 10^{-38} \cdot 6.28} \over {6.626 \times 10^{-34}} } $ , 同样解得$ v_{0} \approx {2.18 \times 10^6}(m/s) $ 。
于是有$ \omega_{0} = { {v_{0} \over r } } \approx {4 \times 10^{16}} $ (Hz), 其中 $ r = a_{0} = { 0.53 \times {10^{-10}} } $ (m) , 这个频率相应波长$ \lambda = { {c \over \omega} \cdot {2 \pi} } = { c \cdot {r \over v} \cdot {2 \pi} } \approx {400 \times 10^{-10}} $ m 。 )