In quantum physics, one principle of Bohr model is: an atom doesn't radiate in stationary states e.g. ground state.
Also the textbooks of electrodynamics said:"The atom is stable in ground state and doesn't emit radiation, this is in profound
contradiction with classical electrodynamics". For according to the Rutherford model of atom, the electron in circular motion
inside the atom will continuously emit electromagnetic radiation, so it will lose all its energy in a very short time. Such that
the atom is not stable and will collapse. I do some calculation supposing the electron of the hydrogen atom is in circular motion
on the circle of Bohr radius(n=1), then the circular frequency is of the magnitude $10^{16}$ $^{\dagger\dagger}$ .
If the electron was able to emit electromagetic radiation as to classical electrodynamics and emit at this frequency, then
the corresponding wavelength is serveral hundred angstrom, a higher frequency than the visible light's.(The atom dimension is of 1Å,
the visible light's wavelength is about several thousand Å). In the book New Concept Physics - Quantum Physics(in Chinese) it said:"
If there isn't energy supplementation, the orbit of the electron will shrink continuously and finally be attracted onto the nucleus."
I browsed some contents of the books Berkeley Physics Course volume 3 - Waves and The M.I.T Introductory Physics Series - Vibrations
and Waves and got to know that, not only in quantum mechanics but also in classical mechanical vibration, there is the concept of eigenstate,
e.g. standing wave state. So I asked: Can it change from a non-standing wave state to standing wave state? What are the changes among
standing wave eigenstates like? How can it change from a non-standing wave state to standing wave state(such as reflection)? How can
a standing wave eigenstate change to a non-standing wave state and subsequently change to another standing wave eigenstate?
It is generally spoken that the standing wave doesn't propagate energy. In fact we should say the standing wave doens't absorb/release
net energy. In the book New Concept Physics - Quantum Physics(in Chinese) it said:"How to ... form a standing wave? Generally it
relies on reflection". The energy propagation of the vibration cannot penetrate the potential barrier, the wave is fully reflected
by the barrier, then the two form a superposition, thus the standing wave. So at the beginning I consider if there is some mechanism
for the electromagnetic wave that the electron(e.g. in the hydrogen atom) radiates being reflected/scattered by potential barrier.
Suppose then it is reabsorbed by the electron so that, in consequence, when we observe from outside, we find there isn't any energy
transmitted out of the potential barrier(thus we reckon Bohr's saying right: the hydrogen atom in ground state doesn't radiate).
But this thought seems to be rather far from the reality( that I know). Considering the surroundings the electron lies in, it is not
heard of that something could reflect back the electromagnetic wave the electron emits. Even if there is, how could the electron happen to
fully reabsorb it? This picture is rather strange(maybe electromagnetic damping can be considered). But considering the surroundings the
electron being in, I think: in reality, the charged particles(e.g. the electrons) are always in the heat radiation field, so they have to
vibrate, absorb and radiate. Thus I consider how to learn how many the electrons absorb from the electromagnetic field(e.g. considering
the picture that a hydrogen atom being put inside a black-body radiation cavity). This is also some knowledge about heat radiation and
equilibrium. I did some searching in some books on microwaves and seemingly it didn't benefit. One day, I read about the deduction of
Rayleigh-Jean's formula in Ta-You Wu's book and I felt I found the answer of my question.
This deduction shows that the energy being absorbed from the electromagnetic field by the electron can happen to be equal to the
energy that it radiates. So I regard it now that the electron inside the atom doesn't necessarily radiate nothing, it just takes
equilibrium between radiation and absorption.
${\overline p = {1 \over {4 \pi \epsilon_{0}}} { {e^2 a^2 \omega^4} \over {3 c^3} }}$
(electrodynamics textbooks)
(electrodynamics textbooks)
( $\psi = {1 \over {4 \pi \epsilon_{0}}} w $ ?)
((There is also a formula named Parseval equality in Sturm-Liouville problem, see Mathematical Thought from Ancient to Modern Times ))
the integral domain enlarged to be a rectangle
$\psi_{\nu} d \nu = {8 \pi kT \over c^3 } \nu^2 d \nu $
In the appendix two (page 18) of Ta-You Wu's book Theoretical Physics - Quantum Theory And Atom Structure(in Chinese, below I will try my best to translate it into English) it wrote:
"
The Rayleigh-Jeans law can also be obtained from pure electrodynamics.
The radiation power of a one-dimensional linear harmonic oscillator is: $$ \begin{aligned} p & = { \omega_{0}^4 (ea)^2 \over 3c^3 } \\ & = { 2 \omega_{0}^2 e^2 \over 3mc^3 } \epsilon, \space \space \space \space \space \space \epsilon = {1 \over 2} m(a \omega_{0})^2 \end{aligned} \tag{I-32/I-32a} $$ $\epsilon$ is the energy of the oscillator.
Now we calculate the power of energy absorption of a linear harmonic oscillator in the electromagnetic field. Assuming the frequency of the oscillator is $\omega_{0}$, same as equality (10), the equation of motion of it in the electric field E is $$ \begin{aligned} \ddot{x} + \omega_{0}^2 x = {e \over m} E_{x} \end{aligned} \tag{I-33} $$
Suppose that in between $ 0 \leqslant t \leqslant T $, the x component $E_{x}$ of $\vec{E}$ can be conducted Fourier transformation as below $$ \begin{aligned} E_{x}(t) & = {1 \over 2\pi} \int_{- \infty}^{\infty} f(\omega) e^{i \omega t} d \omega \\ f(\omega) & = \int_{0}^{T} E_{x}(t) e^{-i \omega t} dt \\ E_{x}(t) & = 0 \space \space \space \space \space \space {t \lt 0} \space \space \space {t \gt T} \end{aligned} \tag{I-34} $$
The condition of $E_{x}(t)$ being a real number is $$ \begin{aligned} f^{*}(\omega) = f(- \omega) \end{aligned} \tag{I-35} $$
$E_{y}(t)$、$E_{z}(t)$ components are alike. According to electrodynamics, the density of the radiation energy of this electromagnetic field, $\psi$, is an average(average as to time) as below $$ \begin{aligned} \psi & = {1 \over {8 \pi} } {\overline {(E^2 + H^2)}} = {1 \over {4 \pi} } {\overline {E^2}} \\ & = {3 \over {4 \pi} } {\overline {E_{x}^2}} \end{aligned} \tag{I-36} $$
From equality (34), we then get: $$ \begin{aligned} {\overline {E_{x}^2}} & = {1 \over T} \int_{0}^{T} {E_{x}}^2 dt \\ & = {1 \over {2 \pi T}} \int_{0}^{T} E_{x} dt \int_{- \infty}^{\infty} f(\omega) e^{i \omega t} d {\omega} \\ & = {1 \over {2 \pi T}} \int_{- \infty}^{\infty} f(\omega) d {\omega} \int_{0}^{T} E_{x} e^{i \omega t} dt \\ & = {1 \over {2 \pi T}} \int_{- \infty}^{\infty} f(\omega) f^{*}(\omega) d {\omega} \\ & = {1 \over {\pi T}} \int_{0}^{\infty} {|f(\omega)|}^2 d \omega \end{aligned} $$
So the energy density between $\omega$ and $\omega + d \omega$ $(\omega = 2 \pi \nu)$ is $$ \begin{aligned} \psi_{\omega} & = {3 \over {4 \pi^2 T}} {|f(\omega)|}^2 \\ or \space \psi_{\nu} & = {3 \over {2 \pi T}} {|f(\nu)|}^2 \end{aligned} \tag{I-37} $$
The solution of equation (33) is $$ \begin{aligned} x(t) & = {e \over {\omega_{0} m}} \int_{0}^{t} E_{x}(\xi) \sin{ \omega_{0} } (t - \xi) d \xi \\ x(0) & = \dot{x} (0) = 0 \end{aligned} \tag{I-38} $$
The work that $E_{x}$ does to the oscillator in one second is $$ \begin{aligned} \Delta{\omega} & = {e \over T} \int_{0}^{T} \dot{x} E_{x} dt \\ & = {e^2 \over {mT} } \int_{0}^{T} E_{x}(t) dt \int_{0}^{t} E_{x}(\xi) \cos{ \omega_{0} } (t - \xi) d \xi \\ & = {e^2 \over {mT} } \int_{0}^{T} E_{x}(\xi) d \xi \int_{\xi}^{T} E_{x}(t) \cos{ \omega_{0} } (t - \xi) dt \space \space \space \space \space \space \space \space \dagger \\ & = {e^2 \over {2mT} } \int_{0}^{T} E_{x}(t) dt { \left \{ \int_{0}^{t} + \int_{t}^{T} \right \} } E_{x}(\xi) \cos{ \omega_{0} } (t - \xi) d \xi \\ & = {e^2 \over {4mT} } { \left \{ {\int_{0}^{T} E_{x}(t) e^{i \omega_{0} t} dt \int_{0}^{T} E_{x}(\xi) e^{-i \omega_{0} \xi} d \xi + \int_{0}^{T} E_{x}(t) e^{-i \omega_{0} t} dt \int_{0}^{T} E_{x}(\xi) e^{i \omega_{0} \xi} d \xi } \right \} } \\ & = {e^2 \over {2mT} } {|f(\omega)|}^2 \space \space \space \space \space \space \space \space \text{ as per (34)} \\ & = {{\pi e^2} \over {3m}} \psi_{\nu} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \text{ as per (37)} \end{aligned} \tag{I-39} $$
Under stable state, the radiation power (32) of the linear harmonic oscillator must be equal to its absorption power (39), that is $$ \begin{aligned} \psi_{\nu} = { {8 \pi \nu^2} \over c^3 } \epsilon \end{aligned} $$
If we apply the "equipartition theorem" in classical physics, $\epsilon = kT $, to this equality, then we obtain the Rayleigh-Jeans law.
$\dagger$ note:
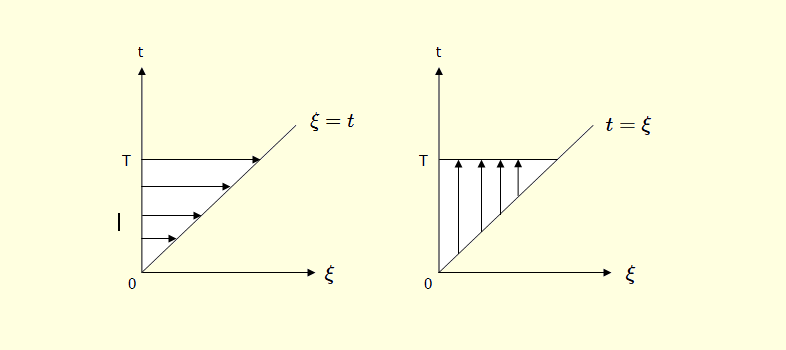
The integral $ \int_{0}^{T} E(t)dt \int_{0}^{t} E(\xi) \cos \omega (t - \xi) d \xi $ is the area marked by the horizontal lines in the picture which is on below left side,
The integral $ \int_{0}^{T} E(\xi)d \xi \int_{\xi}^{T} E(t) \cos \omega (t - \xi) dt $ is the area marked by the vertical lines in the picture which is on below right side. So the above two expressions are equal.
"
[References]
Theoretical Physics - Quantum Theory And Atom Structure by Ta-You Wu (in Chinese)
Men of Physics: Lord Rayleigh - The Man and his Work by Robert Bruce Lindsay
https://en.wikipedia.org/wiki/John_William_Strutt,_3rd_Baron_Rayleigh
https://en.wikipedia.org/wiki/Rayleigh-Jeans_law
Advanced Concepts in Quantum Mechanics (Appendix 2.A) by Giampiero Esposito (p46)
It is said that Rayleigh deduced it which is known as Rayleigh-Jeans law today using equipartition theorem in 1900, and
in 1905 Rayleigh and Jeans gave a more complete deduction and minor corrections. I didn't find their original papers(it will be
appreciated if you can offer them). I don't know if they used pure electrodynamics in their paper as Ta-You Wu says it here.
I can't find equality (10) it says here.
(density is average by the whole space volume?)
( $ E_{x}$, $ E_{y}$, $ E_{z}$ ?)
( $ E_{x}$, $ E_{y}$, $ E_{z}$ ?)
Parseval equality holds for Fourier transformation:
$$ \begin{aligned} \int_{-\infty}^{\infty} {|f(\omega)|}^2 d \omega \end{aligned} $$ $$ \begin{aligned} = 2 \pi \int_{-\infty}^{\infty} {|g(x)|}^2 dx \end{aligned} $$
$$ \begin{aligned} \int_{-\infty}^{\infty} {|f(\omega)|}^2 d \omega \end{aligned} $$ $$ \begin{aligned} = 2 \pi \int_{-\infty}^{\infty} {|g(x)|}^2 dx \end{aligned} $$
$$
\begin{aligned}
\psi & = {3 \over 4 \pi^2 T }\int_{0}^{\infty} {|f(\omega)|}^2 d \omega \space \space \space \text{;} \\
& = \int_{0}^{\infty} \psi_{\omega} d \omega \\
& = \int_{0}^{\infty} \psi_{\nu} d \nu
\end{aligned}
$$
It is extremely wonderful to get this solution. I don't know how and can only verify this solution,
applying the derivative formula of the integral with parameter variables in calculus:
$$
\begin{aligned}
{d \over dx } \int_{\alpha (x)}^{\beta (x)} f(x,y)dy
\end{aligned}
$$
$$
\begin{aligned}
& = \int_{\alpha (x)}^{\beta (x)} { {\partial f(x,y)} \over {\partial x}} dy \\
& + f[x, \beta (x)] \beta^{\prime}(x) \\
& - f[x, \alpha (x)] \alpha^{\prime}(x)
\end{aligned}
$$
The Fourier transformation in real number form:
$$
\begin{aligned}
f(t) = {1 \over \pi } \cdot
\end{aligned}
$$
$$
\begin{aligned}
\int_{0}^{\infty} d \omega \int_{- \infty}^{\infty} f(\tau) \cos \omega (t- \tau) d \tau
\end{aligned}
$$
Errata of the original book:
In the book version I use the words: $$ \begin{aligned} E(t) \cos \omega (t - \xi) dt \end{aligned} $$ inside the latter expression was mistaken as: $$ \begin{aligned} E(t) \cos \omega (t - \xi) d \xi \end{aligned} $$
In the book version I use the words: $$ \begin{aligned} E(t) \cos \omega (t - \xi) dt \end{aligned} $$ inside the latter expression was mistaken as: $$ \begin{aligned} E(t) \cos \omega (t - \xi) d \xi \end{aligned} $$
I did some calculation to understand the above contents.
(1) About the radiation power of the harmonic oscillator
According to the formula in electrodynamics textbooks, the radiation power of an accelerating charge $$ \begin{aligned} P = {1 \over {4 \pi \epsilon_{0}}} {2 \over 3} { {e^2 {\dot{\vec v}}^2} \over c^3 } \end{aligned} $$ Notate the energy of the harmonic oscillator as $ W = {1 \over 2} m {\dot{z}}^2 + {1 \over 2} k z^2 = {1 \over 2} m a^2 {\omega}^2 $ , suppose $z = a \cos {\omega t} $ , such that $\vec v = \dot z = -a \omega \sin {\omega t} $ , $ \dot{\vec v} = \ddot z = -a {\omega}^2 \cos {\omega t} $ , so $ P = {1 \over {4 \pi \epsilon_{0}}} {2 \over 3} { e^2 a^2 {\omega}^4 {\cos}^2 {\omega t} \over c^3 } $ .
To calculate the average value $ {1 \over T} \int_{0}^{T} {\cos}^2 {\omega t} dt $ , applying $ T = {1 \over \nu} = { {2 \pi} \over \omega } $ , which is $ 1 \over 2 $ , so we have ${\overline p = {1 \over {4 \pi \epsilon_{0}}} { {e^2 a^2 \omega^4} \over {3 c^3} }}$. The scale factor is for the difference between systems of units, thus we have the equality of radiation power in the original text.
(2) About the verification of the solution of equation (33)
As the sidenote, by directly applying the formula we get: $$ \begin{aligned} \dot x & = {e \over {\omega_{0} m}} \int_{0}^{t} \omega_{0} E_{x}(\xi) \cos {\omega_{0} (t - \xi) d \xi} + E_{x}(t) \sin \omega_{0}(t-t) \\ \ddot x & = { {e \omega_{0}} \over {\omega_{0} m} } \left [ \int_{0}^{t} \omega_{0} E_{x}(\xi) (- \sin {\omega_{0} (t - \xi)) d \xi} + E_{x}(t) \cos \omega_{0}(t-t) \right ] \end{aligned} $$ substitute onto the left side and we are done.
(3) About the verification of one step in (I-39)
Changing the variable symbol in the integral $$ \begin{aligned} \int_{0}^{T} E_{x}(\xi) d \xi \int_{\xi}^{T} E_{x}(t) \cos{ \omega_{0} } (t - \xi) dt \end{aligned} $$ will not affect its value. By exchanging the symbols $ t $ and $ \xi $ $$ \begin{aligned} \int_{0}^{T} E_{x}(t) dt \int_{t}^{T} E_{x}(\xi) \cos{ \omega_{0} } (\xi - t) d \xi \end{aligned} $$ ,thus we have the middle step in the original text.
(4) About equality (I-37)
I haven't understood it well. I doubt it should be $ \psi_{\nu} = {3 \over {2 \pi T}} {|f(\omega)|}^2 = {3 \over {2 \pi T}} {|f(2 \pi \nu)|}^2 $ , and the end of equality (I-39) behind seems to support this, too.
Why I felt I found the answer? Well, this deduction starts from the point that the radiation power equals the absorption power,
and gets the Rayleigh-Jeans formula deduced. Good, now that we know the Rayleigh-Jeans law holds(at least holds in some range(long wave part,
low frequency?)), so if we deduce starting from it, naturally we will have that the radiation power equals the absorption power.
This is right what I need.
Likewise, the electron doesn't necessarily radiate nothing in any eigenstate, it is just in a dynamic equilibrium between radiation and absorption.
(In the case of short-life excited state, the equilibrium lasts very short. Why does the excited eigenstate transfer to the ground state so soon?
The mechanic vibration seems different(?). Why isn't the excited eigenstate (thermal) equilibrium state?).
If I have resources to conduct experiments, I will first follow this direction.
$\dagger\dagger$ (Applying some formulae: $ m_{e} {v^2 \over r} = k {e^2 \over r^2} $, take r as Bohr radius, $ r = a_{0} = {4 \pi \epsilon_{0}} {{\hbar}^2 \over {m_{e} e^2} } $ , thus we have $ v_{0}^2 = { {k^2 e^4} \over {\hbar}^2 } $ , the kinetic energy $ T = { {1 \over 2} m_{e} v^2 } = { {1 \over 2} { m_{e} {k^2 e^4} \over {\hbar}^2 } } $ , the potential energy $ U = -k {e^2 \over r} = -k^2 {m_{e} \over {\hbar}^2} e^4 $ :
It can be seen that $ T = -{1 \over 2} U $ . The energy of the electron in ground state $ -13.6eV=T+U=-T={1 \over 2} U $ . Using $ { {1 \over 2} m_{e} v_{0}^2 } = 13.6eV $ we get: $ v_{0}^2 = {2 \times 13.6} \cdot {e \over m_{e}} = {2 \times 13.6} \cdot { {1.6 \times 10^{-19}} \over {9.1 \times 10^{-31}}} $ , solve it and we obtain $ v_{0} \approx {2.18 \times 10^6}(m/s) $ .
Or we can apply that $ v_{0}^2 = { {k^2 e^4} \over {\hbar}^2 } $ , thus $ v_{0} = k \cdot {{e^2 \cdot {2 \pi}} \over h} = 9 \times 10^9 \cdot { {2.56 \times 10^{-38} \cdot 6.28} \over {6.626 \times 10^{-34}} } $ , and we can get the same result $ v_{0} \approx {2.18 \times 10^6}(m/s) $ .
So we have $ \omega_{0} = { {v_{0} \over r } } \approx {4 \times 10^{16}} $ (Hz), in which $ r = a_{0} = { 0.53 \times {10^{-10}} } $ (m) , The wavelength corresponding to this frequency $ \lambda = { {c \over \omega} \cdot {2 \pi} } = { c \cdot {r \over v} \cdot {2 \pi} } \approx {400 \times 10^{-10}} $ m . )