

狭义相对论的公设理解
为理解狭义相对论的公设的意思,最好了解一些电磁学/电动力学(爱因斯坦的论文就名为《论动体的电动力学》或《论运动物体的电动力学》), 相对论的出现也是电磁理论/电动力学认识发展后的历史需要。另外,“波”涉及到三者(波源、媒质、观察者)的关系,“波速”的说法可能有 不同的意思:传播速率/度、反应速度;波前(传播)速率/度,表观速度(《费曼物理学讲义》中的说法)等。
电磁理论之前,牛顿力学符合伽利略力学相对性原理,(参考系变换下物理定律形式不变这样的想法对于高中水平的学生可能觉得新奇之处。) 虽然牛顿力学持绝对时空观/绝对参考系的观点。
电磁理论/电动力学产生发展后,麦克斯韦方程组(1)导出波动方程,得到 $c = {1 \over {\sqrt{\epsilon_0 \mu_0}}}$,问题:该速度相对什么? (2)不符合伽利略变换协/不变。
机械波的波动方程是相对于媒质建立的,得出的波速相对于媒质;历史上人们开始认为电磁波是在“以太”媒质中传播,类比于机械波,认为c仅 相对于静止以太。并且类比于机械波波速,认为光速在地球经受的“以太风”中是各向异性的,对观察者在各个方向上应显示出不同(可参见 《新概念物理 力学》)。于是设计了MM实验来企图发现光速可变,这种想法认为麦克斯韦方程组仅在一特定的参考系(“以太”参考系)成立, “以太”参考系成为优越的“绝对参考系”,由此可探知“绝对运动”。但MM实验的企图失败了。
另外的出路即坚持电磁现象也服从相对性原理,麦克斯韦方程组形式正确,不存在优越的惯性系,参考系变换应改变(即使用洛伦兹变换), 由此应可导出/理解光速不变:(1)当光源运动不变,类比机械波,这一点较易理解/接受; (2)当观察者运动不变,这一点不易理解/接受;这一点上光速与声速不同。比如通常说声速(对介质)与波源运动无关,但这是指的是声在静止的介质 参考系中,并且观察者(相对介质)静止。一当观察者运动,声速(对观察者) 就可变了(各向异性)。这样,简单的参考系变换(伽利略变换)不能满足, 必须代之以时空相对性的新变换。注意这里光速不变的光速指的应当是电磁波前传播速度(对观测者), 我看的书中好象只有福克的 《空间、时间和引力的理论》显著这样的说明。有的书的作者直接区别了“声速”与“光速”的“速度”一词(在这时)含义不同(参见下面笔记), 指出前者指对于介质的速度,而后者指对于观测者的速度。 (所以汪洁在《时间的形状》p55-56中所指的"光,它的传播速度其实是‘每一个报数的人,他们的反应速度’……火车跑得再快 也应该跟报数人的反应速度无关,我应该仍然看到他们以同样的反应速度传递着1,2,3……才对啊。这么说来,光速相对于任何参照系来说, 应该都是恒定不变的。"的理解未必完全。)
对光,光速(光波前速率)对(惯性)观察者是个常数;对声,声波前对观察者的速度则受三者影响:“相速”($\lambda / T $)+随媒质的速率+ 与观察者靠近(观察者对媒质)的速率。机械波对媒质的波速与波源速度之间不适用伽利略变换速度加法定理,但其波前对观察者的速度适用 伽利略变换速度加法定理。
当然,科学是严谨的。历史上还有如以太曳引、发射理论等许多复杂曲折之处。
光速这一传播速度是物体运动速度的极限,但要注意也有出现c+v(大于c)的地方:
梁绍荣《电动力学基础》p265、(p255、p251): “那么在上面的讨论中,为什么出现(c+v)项?请注意,这并不是静止于S系的观察者看光脉冲对他的速度,而是该观察者看光脉冲 对$a^\prime$的速度,这个速度当然可以大于c,但最大也不能超过2c。”
蔡伯濂《狭义相对论》p45: “可能有些读者会提出,(c+v)不是超光速的吗?是否违背光速不变原理?回答是,不违背光速不变原理。光速不变原理所指的是用 所在惯性系的时钟和尺对真空中光速测量都为c,与光源的运动无关。而这里所讨论的是用S系的时钟和尺测量$B^\prime$光脉冲对 运动着的$P^\prime$的相对速度,其值是完全可以超光速的。”
Forshaw 《Dynamics and Relativity》p114: “An observer in S measures the light to travel towards an observer in $S^\prime$ at a speed c+v.”
《从牛顿定律到爱因斯坦相对论》2ed. p38注: “这里我们又一次遇到光速极限问题,速度c+v显然是超过光速的,但它并不同光速极限相矛盾。光速不变性是说光相对于观察者的速度 不变。而这里的c+v则是观察者看到的一束光与另一物体之间的相对速度,后者是可以超过光速的。”
《狭义相对论》刘辽等p39、p37: “任意物体相对于任意惯性系的速度不能超光速,但在同一惯性系中(或者相对于同一惯性观测者),两个物体的相对速度可以超光速。”
《狭义相对论入门》叶壬癸p90: “必须指出,从‘当事者’看来,速度相‘加’永远不能大于c,但从‘第三者’看来,‘超光速’仍是可能的。……我们前面在计算例题时,也曾 用过光接近第三者的速度大于c的这类事实。比方说,飞船以速度v接近地球,光从地球射向飞船时,从地球看来,光与飞船互相接近 的速度就是c+v。”
(至于麦克斯韦方程组牢固可靠的条件,在老版本(可能是第一版,第二版中就没有了)的赵凯华《电磁学》下卷p296作者曾指出:
“除了涡旋电场和位移电流假说外,他(麦克斯韦)还假设电学的高斯定理和磁学的‘高斯定理’在非稳条件下仍成立,……”)
首要的参考文献:
《光速不变原理的讨论》李小牛等
《空间、时间和引力的理论》福克
对我较有意味的科普书:《改变世界的方程》。
下面是为了理解狭义相对论的两个公设所作的笔记。


















一些更新:




在论坛上问了一下:

有如此回复:

Sommerfeld的书在第四卷(Optics)第22节(114页)。
Jackson的书在第7.11节提到:


上面的网址。
看到张宗燧的《电动力学及狭义相对论》第6章,又有了些新看法:












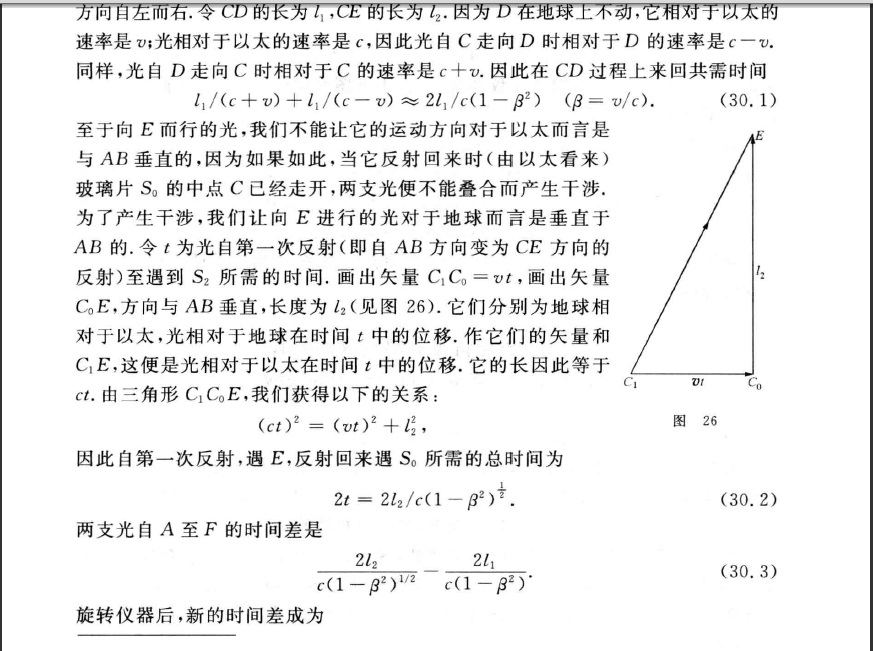



原书电子版在这里下载(电动力学及狭义相对论重排本张宗燧)(请勿用于商业用途)。
其中参考了布洛欣采夫的群速度说明(第20页):










其英文电子版在这里下载(Blokhintsev_Quantum_Mechanics)(请勿用于商业用途)。
胡宁在《电动力学》第56节(p274-275)中写道:
“我们曾经证明,相对论力学定律和电磁现象的定律(即麦克斯韦方程组)在所有的惯性坐标系里都是相同的。这些规律是 在所用坐标系只限于惯性坐标系这个具体条件下的规律。人们自然要问,在任一坐标系里的运动和电磁现象的规律是什么? 换句话说,与坐标系的选择完全无关的更普遍的力学和电动力学的规律是什么?这个规律必然是前面所述规律的进一步的 抽象化。这个抽象化的结果是把这些规律由微分方程的形式提高到变分原理的形式,即对于一个任意的坐标变换来讲,这些 规律将不可能写成相同的微分方程式,但它们却可表成同一个变分原理的形式。由这个变分原理得出的方程式是拉格朗日方程式 或哈密顿方程式。作为具体的微分方程式,拉格朗日方程式和哈密顿方程式在一般的坐标变换下是完全不同的,但把它们看做 拉格朗日函数和哈密顿函数这些‘函数的函数’或‘超函数’所满足的方程式来看时,则它们在一般坐标变换下却又具有相同的形式了。 ”