Here I read one wonderful paper on Ewald-Oseen theorem. Its author is H. Serhat Tetikol. His e-mail is htetikol@ku.edu.tr. I also uploaded one local copy （ppt）。
Here below I marked two places where I don't understand well. I hope I could ask for the author's help.
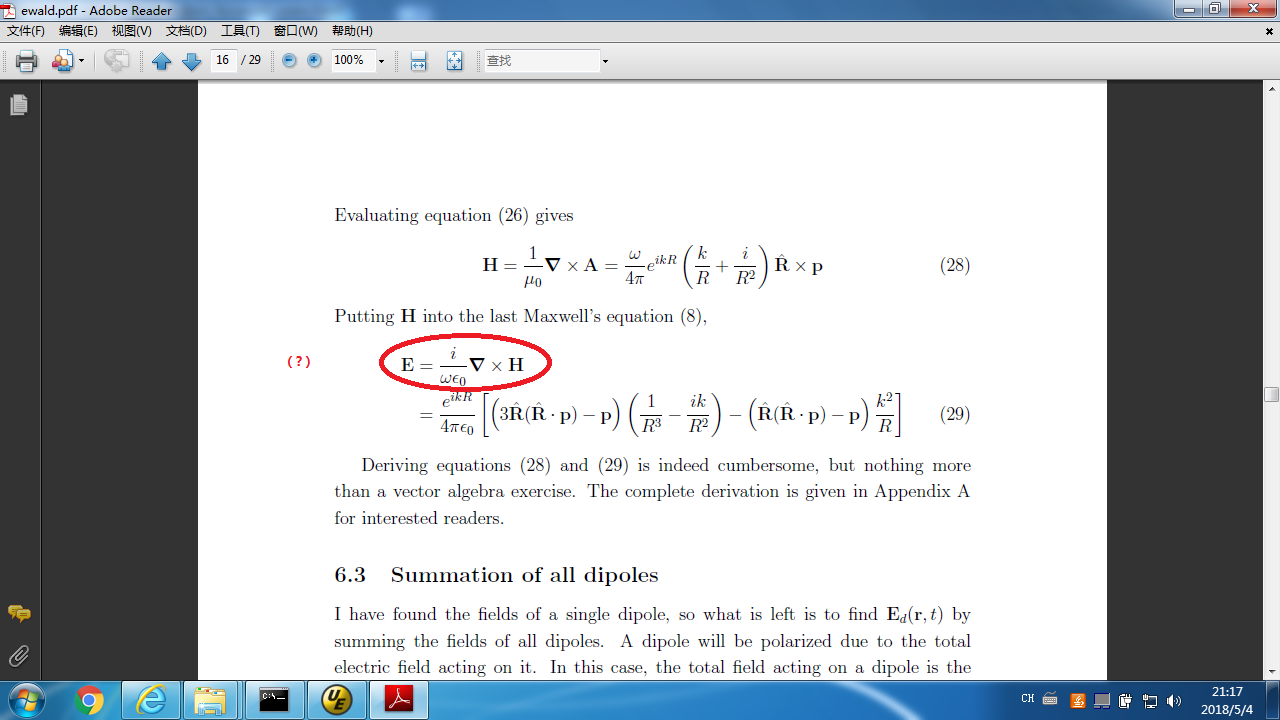Question 1 of mine in the above image: Where does this come from? Is it because:
$$
\begin{aligned}
\nabla \times \vec{H} & = \vec{J_{ext}} + \epsilon_{0} {{\partial \vec{E}}\over{\partial t}} \\
\vec{E} & = E e^{-i\omega t} \\
\text{so that,} \nabla \times \vec{H} & = \vec{J_{ext}} + \epsilon_{0} E e^{-i\omega t} (-i \omega) \\
\vec{E} & = { { \nabla \times \vec{H} - \vec{J_{ext}} } \over {-i \omega \epsilon_{0}} } \\
& = { i \over { \omega \epsilon_{0} } } \nabla \times \vec{H}
\end{aligned}
$$
?
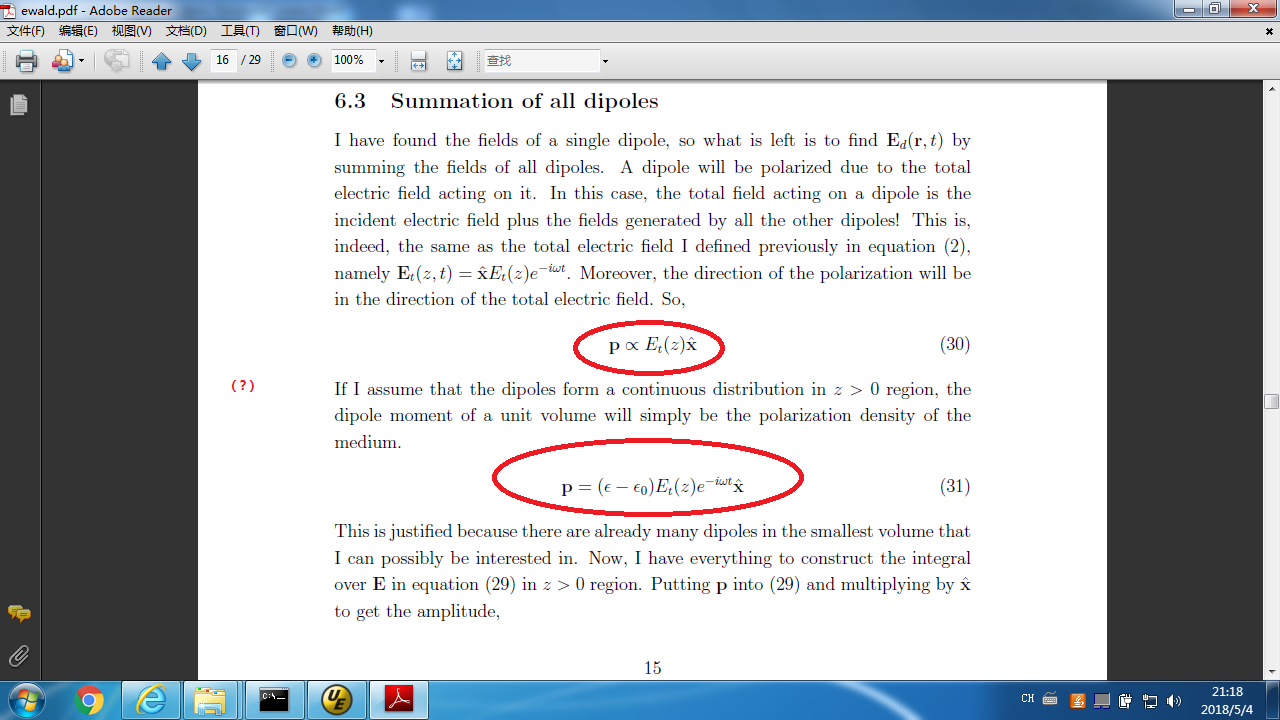Question 2 of mine in the above image: I cannot understand the author's analysis about the proportion relation here.
And how does the $\epsilon$ appear here abruptly? What is the meaning of subtracting $\epsilon_{0}$ from it?
Below is my extraction and translation in Chinese(the question mark is of the above meaning) of the original paper:
(One can skip it if he doesn't want to take a look at Chinese version)
I planned to read Lorentz's paper LA THEORIE ELECTROMAGNETIQUE DE MAXWELL ET SON APPLICATION AUX CORPS MOUVANTS, because someone said that in this paper according to Lorentz's theory when the light passes transparent bodies, the incident light makes the electrons and ions in the substance vibrate, this vibration produces new light waves and they interfere with both the original incident light and themselves. Using this kind of concept, Lorentz deduced the speed of light in the transparent moving media relative to the ether reference frame in 1892. I want to see how he analyzed it. However I don't understand French
(La Th$\acute{e}$orie $\acute{E}$lectromagn$\acute{e}$tique de Maxwell et Son Application Aux Corps Mouvants, DOI:10.1007/978-94-015-3447-5_4), and the the famous master's theoretical thought is very abstract. I spent time on looking up French dictionary but didn't find out what was to seek and could only left it be.
